题目内容
19.若在数列“△,△,△,△,7,△,△,△,47”中,每个△都代表一个数,而且从第三项起,每个数都等于前面两个数之和,求数列中全部9个数之和.分析 首先假设出前三个数据,在分别表示出各数据,进而得出二元一次方程组求出即可
解答 解:设前三个数为a,b,a+b,
根据题意得第4个数为:b+a+b,
第五个数为:(a+b)+a+2b=7,
2a+3b=7,
第6个数是 b+(a+b)+7=a+2b+7,
第7个数是 a+2b+7+7=a+2b+14,
第8个数是 a+2b+14+a+2b+7=2a+4b+21,
第9个数是 2a+4b+21+a+2b+14=3a+6b+35=47,
∴a+2b=4,
∴$\left\{\begin{array}{l}{2a+3b=7}\\{a+2b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$
∴这组数据为:2,1,3,4,7,11,18,29,47.
∴2+1+3+4+7+11+18+29+47=122,
∴这9个数的和为122.
点评 本题主要考查的是二元一次方程组的应用,根据题意列出方程组是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
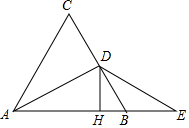 如图,在等边三角形ABC中,D是BC边的中点,E是AB延长线上的一点,且BE=BD,过点D作DH⊥AB于H.
如图,在等边三角形ABC中,D是BC边的中点,E是AB延长线上的一点,且BE=BD,过点D作DH⊥AB于H.