题目内容
9.某商场打折促销某种商品,已知该商品的进价是420元,商场规定按高于进价的$\frac{1}{2}$标价,为了商场正常运转,商品的利润应不低于进价的20%,如果你是店长,该商品最低能打几折?分析 由题意可知:利润率为20%时,获得的利润为420×20%=84元;若打x折该商品获得的利润=该商品的标价×0.1x-进价,即该商品获得的利润=420×(1+$\frac{1}{2}$)×0.1x-420,列出不等式,解得x的值即可.
解答 解:设可以打x折出售此商品,由题意得:
420×(1+$\frac{1}{2}$)×0.1x-420≥420×20%,
解得x≥8.
答:该商品最低能打8折.
点评 本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.十六大提出全面建设小康社会.国际上常用恩格尔系数(记作n)来衡量一个国家和地区人民生活水平的状况,它的计算公式为:n=$\frac{食品消费支出总额}{消费支出总额}$×100%
根据上述材料,解答下列问题:
某校初三学生对我市一个乡的农民家庭进行抽样调查.从1997年至2002年间,该乡每户家庭消费支出总额每年平均增加500元,其中食品消费支出总额每年平均增加200元.1997年该乡农民家庭平均刚达到温饱水平,已知该年每户家庭消费支出总额平均为8000元.
(1)1997年该乡平均每户家庭食品消费支出总额为多少元?
(2)设从1997年起m年后该乡平均每户的恩格尔系数为nm(m为正整数).请用m的代数式表示该乡平均每户当年的恩格尔系数nm,并利用这个公式计算2003年该乡平均每户的恩格尔系数(百分号前保留整数).
(3)按这样的发展,该乡将于哪年开始进人小康家庭生活?该乡农民能否实现十六大提出的2020年我国全面进人小康社会的目标?
| 家庭类型 | 贫困 | 温饱 | 小康 | 富裕 | 最富裕 |
| n | n>60% | 50%<n≤60% | 40%<n≤50% | 30%<n≤40% | n≤30% |
某校初三学生对我市一个乡的农民家庭进行抽样调查.从1997年至2002年间,该乡每户家庭消费支出总额每年平均增加500元,其中食品消费支出总额每年平均增加200元.1997年该乡农民家庭平均刚达到温饱水平,已知该年每户家庭消费支出总额平均为8000元.
(1)1997年该乡平均每户家庭食品消费支出总额为多少元?
(2)设从1997年起m年后该乡平均每户的恩格尔系数为nm(m为正整数).请用m的代数式表示该乡平均每户当年的恩格尔系数nm,并利用这个公式计算2003年该乡平均每户的恩格尔系数(百分号前保留整数).
(3)按这样的发展,该乡将于哪年开始进人小康家庭生活?该乡农民能否实现十六大提出的2020年我国全面进人小康社会的目标?
8.若a+b=-1,则a2+b2+2ab的值为( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
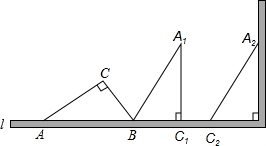 如图,一个横截面为Rt△ABC的物体,∠ACB=90°,∠CAB=30°,BC=1m,工人师傅要把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1BC1的位置(BC1在l上),最后沿射线BC1的方向平移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).
如图,一个横截面为Rt△ABC的物体,∠ACB=90°,∠CAB=30°,BC=1m,工人师傅要把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1BC1的位置(BC1在l上),最后沿射线BC1的方向平移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).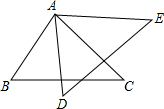 已知:如图,△ABC≌△ADE,∠BAE=110°,∠BAD=40°,则∠BAC=70°.
已知:如图,△ABC≌△ADE,∠BAE=110°,∠BAD=40°,则∠BAC=70°.