题目内容
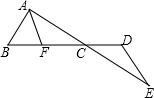 如图,AB=DE,AE、BD相交于点C,AF∥DE交BD于点F,∠B+∠D=180°.求证:CF=CD.
如图,AB=DE,AE、BD相交于点C,AF∥DE交BD于点F,∠B+∠D=180°.求证:CF=CD.考点:全等三角形的判定与性质
专题:证明题
分析:根据两直线平行,内错角相等可得∠D=∠AFC,再根据等角的补角相等求出∠B=∠AFB,根据等角对等边可得AB=AF,从而得到AF=DE,然后利用“角角边”证明△ACF和△ECD全等,根据全等三角形对应边相等可得CF=CD.
解答:证明:∵AF∥DE,
∴∠D=∠AFC,
∵∠B+∠D=180°,∠AFB+∠AFC=180°,
∴∠B=∠AFB,
∴AB=AF,
∵AB=DE,
∴AF=DE,
在△ACF和△ECD中,
,
∴△ACF≌△ECD(AAS),
∴CF=CD.
∴∠D=∠AFC,
∵∠B+∠D=180°,∠AFB+∠AFC=180°,
∴∠B=∠AFB,
∴AB=AF,
∵AB=DE,
∴AF=DE,
在△ACF和△ECD中,
|
∴△ACF≌△ECD(AAS),
∴CF=CD.
点评:本题考查了全等三角形的判定与性质,平行线的性质,等角的补角相等的性质,等角对等边的性质,难点在于求出AB=AF从而求出三角形全等的边的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若a、b、c是三角形的三条边长,则化简
+丨b-a-c丨的结果是( )
| (a-b-c)2 |
| A、-2c | B、2a-2c |
| C、2b | D、2c |
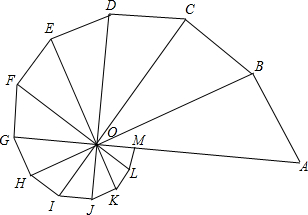 如图所示的图形是由12个有公共顶点O的直角三角形拼成的,∠AOB=∠BOC=…∠LOM=30°.你能从图中找出与△ABO位似的图形吗?它们的位似比是多少?
如图所示的图形是由12个有公共顶点O的直角三角形拼成的,∠AOB=∠BOC=…∠LOM=30°.你能从图中找出与△ABO位似的图形吗?它们的位似比是多少?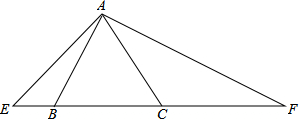 已知∠EAF=120°,它绕着边长为2的正△ABC的顶点A旋转,在正△ABC的左侧,右侧分别交直线BC于E,F.求BE•CF的值.
已知∠EAF=120°,它绕着边长为2的正△ABC的顶点A旋转,在正△ABC的左侧,右侧分别交直线BC于E,F.求BE•CF的值.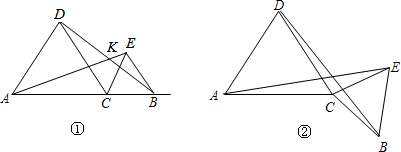
 如图,在⊙O中,BC、CD为⊙O的弦,过O作OA⊥BC交⊙O于点A,连接AD,若∠CDA=25°,∠AOB的度数是多少?
如图,在⊙O中,BC、CD为⊙O的弦,过O作OA⊥BC交⊙O于点A,连接AD,若∠CDA=25°,∠AOB的度数是多少?