题目内容
已知关于x的方程x2+px+q=0的根分别满足下列条件,试求出系数p、q应满足的条件.
①两根互为倒数;
②两根互为相反数;
③有一根为0;
④有一根为1.
①两根互为倒数;
②两根互为相反数;
③有一根为0;
④有一根为1.
考点:根与系数的关系,一元二次方程的解
专题:
分析:(1)根据判别式的意义和两根之积得到△=p2-4q≥0且q=1,然后解不等式即可;
(2)根据判别式的意义和两根之和得到△=p2-4q≥0且-p=0,然后解不等式即可;
(3)根据一元二次方程解的定义把x=0代入原方程即可得到q=0;
(4)根据一元二次方程解的定义把x=1代入原方程即可得到P+q=-1.
(2)根据判别式的意义和两根之和得到△=p2-4q≥0且-p=0,然后解不等式即可;
(3)根据一元二次方程解的定义把x=0代入原方程即可得到q=0;
(4)根据一元二次方程解的定义把x=1代入原方程即可得到P+q=-1.
解答:解:(1)根据题意得△=p2-4q≥0且q=1,
所以q=1,p≥2或p≤-2;
(2)根据题意得△=p2-4q≥0且-p=0,
所以p=0,q≤0;
(3)根据题意得q=0;
(4)把x=1代入原方程得p+q=-1.
所以q=1,p≥2或p≤-2;
(2)根据题意得△=p2-4q≥0且-p=0,
所以p=0,q≤0;
(3)根据题意得q=0;
(4)把x=1代入原方程得p+q=-1.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
学校为了推行阳光体育活动新购进一大批篮球,可以平均分给初一(x-3)个班也可以平均分给初二(x-2)个班(x是大于3的自然数),用代数式表示这一大批篮球的数量不可能是( )
| A、2(x-2)(x-3) |
| B、x2-5x+6 |
| C、x3-5x2+6x |
| D、x2+5x-6 |
 如图,正方形ABCD中,∠EAF=45°,BE=2,FC=6,求EF的长.
如图,正方形ABCD中,∠EAF=45°,BE=2,FC=6,求EF的长.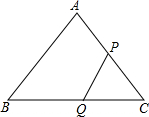 如图,在△ABC中,AB=AC=25cm,BC=30cm,点P从点C出发,沿CA以2.5cm/s的速度向点A运动.同时点Q从B点出发沿BC以4cm/s的速度向C运动,PQ中有一点到达终点时,两点同时停止运动,设运动时间为t.
如图,在△ABC中,AB=AC=25cm,BC=30cm,点P从点C出发,沿CA以2.5cm/s的速度向点A运动.同时点Q从B点出发沿BC以4cm/s的速度向C运动,PQ中有一点到达终点时,两点同时停止运动,设运动时间为t.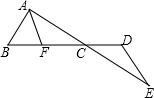 如图,AB=DE,AE、BD相交于点C,AF∥DE交BD于点F,∠B+∠D=180°.求证:CF=CD.
如图,AB=DE,AE、BD相交于点C,AF∥DE交BD于点F,∠B+∠D=180°.求证:CF=CD. 观察下图,图中有多少同位角、内错角、同旁内角?请把它们列出来.
观察下图,图中有多少同位角、内错角、同旁内角?请把它们列出来. 如图∠AOB=80°,OD是∠AOB的角平分线,∠AOC=3∠BOC,求∠COD的度数.
如图∠AOB=80°,OD是∠AOB的角平分线,∠AOC=3∠BOC,求∠COD的度数.