题目内容
13.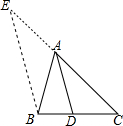 有人猜想三角形内角平分有这样一个性质:如图,在△ABC中,AD平分∠BAC,则$\frac{BD}{CD}$=$\frac{AB}{AC}$.如果你认为这个猜想是正确的,请写出一个完整的推理过程(利用图中辅助线:作BE∥AD交CA延长线于E)说明这个猜想的正确性.
有人猜想三角形内角平分有这样一个性质:如图,在△ABC中,AD平分∠BAC,则$\frac{BD}{CD}$=$\frac{AB}{AC}$.如果你认为这个猜想是正确的,请写出一个完整的推理过程(利用图中辅助线:作BE∥AD交CA延长线于E)说明这个猜想的正确性.
分析 根据平行线的性质和等腰三角形的判定得到AB=AE,再据平行线分线段成比例定理即可得到答案.
解答 证明:∵BE∥AD,
∴∠ABE=∠BAD,∠E=∠CAD,BD:CD=AE:AC,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠ABE=∠E,
∴AB=AE,
∴$\frac{BD}{CD}$=$\frac{AB}{AC}$.
点评 本题考查的是等腰三角形的判定、平行线的性质、平行线分线段成比例定理;熟练掌握平行线分线段成比例定理,证明AB=AE是解决问题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
3. 如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )
如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )
 如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )
如图,在Rt△ABC中,∠C=90°,ED是AB的垂直平分线,交AC于点D,交AB于E,已知∠CBD=10°,则∠A的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
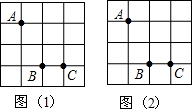
1.如图,已知方格纸中有A、B、C三个格点,求作一个以A、B、C为顶点的格点四边形.
(1)在图1中作出的四边形是中心对称图形但不是轴对称图形.
(2)在图2中作出的四边形是轴对称图形但不是中心对称图形.
(1)在图1中作出的四边形是中心对称图形但不是轴对称图形.
(2)在图2中作出的四边形是轴对称图形但不是中心对称图形.

18.若多项式x2-x-20分解为(x-a)(x-b),则a,b分别为( )
| A. | a=4,b=5 | B. | a=-4,b=5 | C. | a=4,b=-5 | D. | a=-4,b=-5 |
19.关于x的一元二次方程ax2+bx=6的一个根为x=2,则代数式4a+2b的值是( )
| A. | 3 | B. | 6 | C. | 10 | D. | 12 |
 如图,六边形ABCDEF中,AF=CD,AB=DE,FE=BC,∠B=∠E,求证:AF∥CD.
如图,六边形ABCDEF中,AF=CD,AB=DE,FE=BC,∠B=∠E,求证:AF∥CD. 抛物线y=x2+bx+3与x轴正半轴交于A、B两点,(A点在B点左边),与y轴正半轴交于C点,对称轴为x=2,求抛物线的解析式.
抛物线y=x2+bx+3与x轴正半轴交于A、B两点,(A点在B点左边),与y轴正半轴交于C点,对称轴为x=2,求抛物线的解析式.