题目内容

1．已知抛物线的顶点坐标是（2，1），与y轴的交点是（0，-3）．
（1）求这个二次函数的解析式；
（2）求抛物线与x轴两个交点的坐标．

分析 （1）根据抛物线的顶点坐标是（2，1），设抛物线解析式为：y=a（x-2）2+1，把y轴的交点是（0，-3）代入即可求出a的值；
（2）令y=0解出的值即为与x轴的交点．

解答 解：（1）根据抛物线的顶点坐标是（2，1），设抛物线解析式为：y=a（x-2）2+1，
把y轴的交点是（0，-3）代入得：a（0-2）2+1=-3，解得a=-1，
∴y=-（x-2）2+1，即 y=-x2+4x-3；

（2）令  y=-x2+4x-3=0，
解得：x1=1，x2=3，
故与x轴的交点（1，0），（3，0）．

点评 本题考查了待定系数法求二次函数解析式、抛物线与x轴的交点坐标，令y=0，即ax2+bx+c=0，解关于x的一元二次方程即可求得交点横坐标．

练习册系列答案
相关题目
11．二次根式计算：
（1）$\sqrt{9a}+\sqrt{25a}$；
（2）$\sqrt{75}-\sqrt{54}+\sqrt{96}-\sqrt{108}$；
（3）（$\sqrt{48}+\frac{1}{4}\sqrt{6}$）÷$\sqrt{27}$；
（4）（2$\sqrt{3}$$+\sqrt{6}$）（2$\sqrt{3}$$-\sqrt{6}$）．
12．抛物线y=-x2-2x+49的图象如图所示．
（1）若y=25时，求x的值；
（2）若y＞25时，求x的取值范围．
9．计算：
（1）|-12|÷（-3）；
（2）（-$\frac{1}{12}$+$\frac{1}{3}$-$\frac{1}{2}$）÷（-$\frac{1}{18}$）．
16．如图，⊙O的直径AB垂直于弦CD，垂足为E，AE=1，CD=2$\sqrt{3}$．
（1）求AB的长；
（2）连结BC和BD，请判断△BCD的形状，并证明．
6．计算：
（$\sqrt{2}-1$）2（$\sqrt{2}+1$）2（$\sqrt{3}-\sqrt{2}$）2（$\sqrt{3}$$+\sqrt{2}$）2．
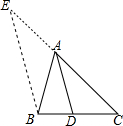13．有人猜想三角形内角平分有这样一个性质：如图，在△ABC中，AD平分∠BAC，则$\frac{BD}{CD}$=$\frac{AB}{AC}$．如果你认为这个猜想是正确的，请写出一个完整的推理过程（利用图中辅助线：作BE∥AD交CA延长线于E）说明这个猜想的正确性．
6．在Rt△ABC中，∠ABC=2∠ACB，延长AB至点D，使BD=BC，点E是直线BC上一点，点F是直线AC上一点，连接DE．连接EF，且∠DEF=∠DBC．
（1）如图1，若∠D=∠EFC，AB=$\sqrt{3}$，求AC的长．
（2）如图2，当∠BAC=45°，点E为线段BC的延长线上，点F在线段AC的延长线上时，求证：CF=$\sqrt{2}$BE．
（3）如图3，当∠BAC=90°，点E为线段CB的延长线上，点F在线段CA的延长线上时，猜想线段CF与线段BE的数量关系，并证明猜想的结论．
7．下列一元二次方程中常数项是0的是（　　）
A．x2-4x=0B．2x2=81C．x2-x=1D．x=4x2+6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网