题目内容
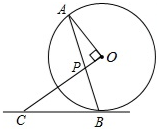 如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P.
如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P.(1)判断△CBP的形状,并说明理由;
(2)若OP=1,PA=
| 10 |
考点:切线的性质
专题:
分析:(1)首先连接OB,由点C在过点B的切线上,且OC⊥OA,根据等角的余角相等,易证得∠CBP=∠CPB,即可证得△CBP是等腰三角形;
(2)由OP=1,PA=
,利用勾股定理可求得OA的长,然后设BC=x,可得方程:x2+32=(x+1)2,解此方程即可求得答案.
(2)由OP=1,PA=
| 10 |
解答: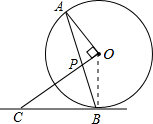 解:(1)△CBP是等腰三角形.
解:(1)△CBP是等腰三角形.
理由:连接OB,
∵BC是⊙O的切线,
∴OB⊥BC,
∴∠OBA+∠CBP=90°,
∵OC⊥OA,
∴∠A+∠APO=90°,
∵OA=OB,
∴∠A=∠OBA,
∴∠APO=∠CBP,
∵∠APO=∠CPB,
∴∠CPB=∠ABP,
∴CP=CB,
即△CBP是等腰三角形;
(2)∵OP=1,PA=
,
∴OA=
=3,
∴OB=OA=3,
设BC=x,则OC=CP+OP=x+1,
在Rt△OBC中,BC2+OB2=OC2,
∴x2+32=(x+1)2,
解得:x=4,
∴BC=4.
 解:(1)△CBP是等腰三角形.
解:(1)△CBP是等腰三角形.理由:连接OB,
∵BC是⊙O的切线,
∴OB⊥BC,
∴∠OBA+∠CBP=90°,
∵OC⊥OA,
∴∠A+∠APO=90°,
∵OA=OB,
∴∠A=∠OBA,
∴∠APO=∠CBP,
∵∠APO=∠CPB,
∴∠CPB=∠ABP,
∴CP=CB,
即△CBP是等腰三角形;
(2)∵OP=1,PA=
| 10 |
∴OA=
| PA2-OP2 |
∴OB=OA=3,
设BC=x,则OC=CP+OP=x+1,
在Rt△OBC中,BC2+OB2=OC2,
∴x2+32=(x+1)2,
解得:x=4,
∴BC=4.
点评:此题考查了切线的性质、勾股定理以及等腰三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
下列四个函数中,y随x的增大而减小的是( )
| A、y=3x | ||
| B、y=x2(x<0) | ||
| C、y=x+3 | ||
D、y=
|
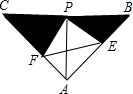 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③BE2+CF2=EF2,④S四边形AEPF=
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③BE2+CF2=EF2,④S四边形AEPF= 如图,已知点C为BD的中点,AB∥DE,∠1=∠2.求证:AF=EG.
如图,已知点C为BD的中点,AB∥DE,∠1=∠2.求证:AF=EG.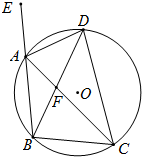 如图,等腰△ABC内接于⊙O,AB=BC,它的外角∠EAC的平分线交⊙O于D点,DB交AC于F.
如图,等腰△ABC内接于⊙O,AB=BC,它的外角∠EAC的平分线交⊙O于D点,DB交AC于F.
 如图,已知∠1=∠2,∠3=∠4,若∠AOE=128°,求∠BOD的度数.
如图,已知∠1=∠2,∠3=∠4,若∠AOE=128°,求∠BOD的度数. 如图,AC是⊙O的直径,OE⊥AB,OF⊥AD,E,F为垂足,OE=OF,AC2=AD•AB,求证:BC是⊙O的切线.
如图,AC是⊙O的直径,OE⊥AB,OF⊥AD,E,F为垂足,OE=OF,AC2=AD•AB,求证:BC是⊙O的切线. 如图是y=a(x+m)2的图象
如图是y=a(x+m)2的图象