题目内容
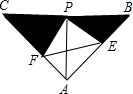 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③BE2+CF2=EF2,④S四边形AEPF=
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③BE2+CF2=EF2,④S四边形AEPF=| 1 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
考点:旋转的性质,全等三角形的判定与性质,勾股定理
专题:
分析:利用旋转的性质可证明△PFA≌△PEB,则有BE=AF,可判定①②③④,利用勾股定理可判断⑤,可得出答案.
解答:解:∵P为BC中点,
∴AP=PB,AP⊥BC,
∵∠EPF=90°,
∴∠FPA+∠APE=∠APE+∠BPE,
∴∠FPA=∠BPE,
在△PFA和△PEB中,
,
∴△PFA≌△PEB(ASA),
∴①正确;
当F旋转到点A时,EF=AB>AP,
∴②不正确;
∵△PFA≌△PEB,
∴AF=BE,且AB=AC,
∴AE=CF,
在Rt△AEF中,AE2+AF2=EF2,
∴BE2+CF2=EF2,
∴③正确;
∵△PFA≌△PEB,
∴S△PFA=S△PEB,
∴S四边形AEPF=S△ABP=
S△ABC,
∴④正确;
又在Rt△PEF和Rt△AEF中,
EF2=PE2+PF2=AE2+AF2,
∴PF2-AF2=AE2-PE2,
∴⑤正确;
综上可知正确的为①③④⑤共四个,
故选C.
∴AP=PB,AP⊥BC,
∵∠EPF=90°,
∴∠FPA+∠APE=∠APE+∠BPE,
∴∠FPA=∠BPE,
在△PFA和△PEB中,
|
∴△PFA≌△PEB(ASA),
∴①正确;
当F旋转到点A时,EF=AB>AP,
∴②不正确;
∵△PFA≌△PEB,
∴AF=BE,且AB=AC,
∴AE=CF,
在Rt△AEF中,AE2+AF2=EF2,
∴BE2+CF2=EF2,
∴③正确;
∵△PFA≌△PEB,
∴S△PFA=S△PEB,
∴S四边形AEPF=S△ABP=
| 1 |
| 2 |
∴④正确;
又在Rt△PEF和Rt△AEF中,
EF2=PE2+PF2=AE2+AF2,
∴PF2-AF2=AE2-PE2,
∴⑤正确;
综上可知正确的为①③④⑤共四个,
故选C.
点评:本题主要考查旋转的性质和全等三角形的判定和性质,掌握旋转前后的线段相等、角相等是解题的关键,注意勾股定理的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
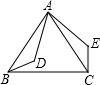 如图,点D是等边△ABC内一点,如果△ABD绕点A逆时针旋转后能与△ACE重合,则∠DAE的度数是( )
如图,点D是等边△ABC内一点,如果△ABD绕点A逆时针旋转后能与△ACE重合,则∠DAE的度数是( )| A、45° | B、60° |
| C、90° | D、120° |
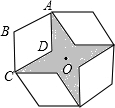 如图是将菱形ABCD以点O为中心分别旋转90°,180°,270°后形成的图形,若∠BAD=60°,AB=2,则图中的阴影部分的面积为( )
如图是将菱形ABCD以点O为中心分别旋转90°,180°,270°后形成的图形,若∠BAD=60°,AB=2,则图中的阴影部分的面积为( )| A、8 | ||
B、12-4
| ||
C、1+
| ||
D、12-2
|
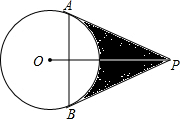 如图,已知PA,PB切⊙O于A、B两点,连AB,∠APB=60°AB=
如图,已知PA,PB切⊙O于A、B两点,连AB,∠APB=60°AB=
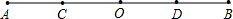 如图,线段AB=6,点O是线段AB上的中点,C、D分别是线段OA、OB的中点,小明据此很轻松得CD=3,他在反思过程中突发奇想:
如图,线段AB=6,点O是线段AB上的中点,C、D分别是线段OA、OB的中点,小明据此很轻松得CD=3,他在反思过程中突发奇想: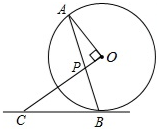 如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P.
如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P.