题目内容
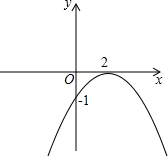 如图是y=a(x+m)2的图象
如图是y=a(x+m)2的图象(1)求二次函数的解析式;
(2)把抛物线y=-
| 1 |
| 4 |
(3)请指出该抛物线的顶点坐标、对称轴及函数具有的性质;
(4)将(1)中所求的抛物线绕顶点旋转180°,求旋转后的抛物线的解析式.
考点:二次函数图象与几何变换,待定系数法求二次函数解析式
专题:
分析:(1)由图象可知,顶点坐标为(2,0),所以可设二次函数的解析式为y=a(x-2)2,再将(0,-1)代入,利用待定系数法即可求解;
(2)根据“左加右减,上加下减”的平移规律即可求解;
(3)根据二次函数的性质即可求出该抛物线的顶点坐标、对称轴及函数具有的性质;
(4)根据图象绕顶点旋转180°,可得函数图象开口方向相反,顶点坐标相同,可得答案.
(2)根据“左加右减,上加下减”的平移规律即可求解;
(3)根据二次函数的性质即可求出该抛物线的顶点坐标、对称轴及函数具有的性质;
(4)根据图象绕顶点旋转180°,可得函数图象开口方向相反,顶点坐标相同,可得答案.
解答:解:(1)由图象可知,顶点坐标为(2,0),所以可设二次函数的解析式为y=a(x-2)2,
将(0,-1)代入,得-1=4a,
解得a=-
,
所以二次函数的解析式为y=-
(x-2)2;
(2)将抛物线y=-
x2向右平移2个单位长度即可得到抛物线y=-
(x-2)2;
(3)∵y=-
(x-2)2,
∴顶点坐标为(2,0),对称轴为x=2,
抛物线开口向下,当x=2时有最大值0,
当x<2时,y随x的增大而增大;当x>2时,y随x的增大而减小;
(4)将(1)中所求的抛物线绕顶点旋转180°,旋转后的抛物线的解析式为y=
(x-2)2.
将(0,-1)代入,得-1=4a,
解得a=-
| 1 |
| 4 |
所以二次函数的解析式为y=-
| 1 |
| 4 |
(2)将抛物线y=-
| 1 |
| 4 |
| 1 |
| 4 |
(3)∵y=-
| 1 |
| 4 |
∴顶点坐标为(2,0),对称轴为x=2,
抛物线开口向下,当x=2时有最大值0,
当x<2时,y随x的增大而增大;当x>2时,y随x的增大而减小;
(4)将(1)中所求的抛物线绕顶点旋转180°,旋转后的抛物线的解析式为y=
| 1 |
| 4 |
点评:本题考查了二次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
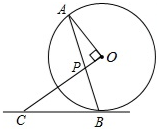 如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P.
如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P. 如图,⊙O与抛物线y=
如图,⊙O与抛物线y= 如图,在一个矩形纸片ABCD剪上减去一个正方形ABEF,所余下的矩形ECDF于原矩形ABCD相似,那么原矩形中较长的边BC与较短的边AB的比是多少?
如图,在一个矩形纸片ABCD剪上减去一个正方形ABEF,所余下的矩形ECDF于原矩形ABCD相似,那么原矩形中较长的边BC与较短的边AB的比是多少?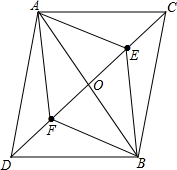 已知,如图,AB与CD相交于点O,AC∥DB,AO=BO,点E、F分别是OC、OD中点,求证:四边形ADBC是平行四边形.
已知,如图,AB与CD相交于点O,AC∥DB,AO=BO,点E、F分别是OC、OD中点,求证:四边形ADBC是平行四边形.