题目内容
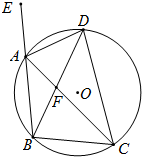 如图,等腰△ABC内接于⊙O,AB=BC,它的外角∠EAC的平分线交⊙O于D点,DB交AC于F.
如图,等腰△ABC内接于⊙O,AB=BC,它的外角∠EAC的平分线交⊙O于D点,DB交AC于F.(1)求证:△DAB≌△DFC;
(2)若cos∠BAC=
| 2 |
| 3 |
| DA |
| DB |
考点:全等三角形的判定与性质,完全平方公式,完全平方式,等腰三角形的性质,圆周角定理,解直角三角形
专题:
分析:(1)易证BD=CD和∠DAB=∠DFC,即可证明△DAB≌△DFC,即可解题;
(2)根据余弦定理可以求得BC2=BD2+CD2-2BD•CD•cos∠BDC和AB2=AD2+BD2-2AD•BDcos∠ADB,根据AB=BC,可以求得
BD2=AD2+BD2-
AD•BD,因式分解即可求得AD,BD的大小关系,即可解题.
(2)根据余弦定理可以求得BC2=BD2+CD2-2BD•CD•cos∠BDC和AB2=AD2+BD2-2AD•BDcos∠ADB,根据AB=BC,可以求得
| 2 |
| 3 |
| 4 |
| 3 |
解答:(1)证明:∵∠DAE+∠DAB=180°,∠DAB+∠DCB=180°,
∴∠DAE=∠DCB,
∴∠DAE=∠DAC,∠DAC=∠DBC,
∴∠DCB=∠DBC,
∴BD=CD,
∵AB=BC,
∴∠ADB=∠FDC,
∵∠DAB=∠DAC+∠BAC,∠DFC=∠DBC+∠BCA,∠BCA=∠BAC,
∴∠DAB=∠DFC,
在△DAB和△DFC中,
,
∴△DAB≌△DFC(AAS);
(2)解:∵∠BAC=∠BDC,∠ADB=∠BDC,
∴∠BDC=∠BAC,
∵在△BDC中有BC2=BD2+CD2-2BD•CD•cos∠BDC,
∴整理得:BC2=
BD2,
∵△ADB中,AB2=AD2+BD2-2AD•BDcos∠ADB,
∴整理得:AB2=AD2+BD2-
AD•BD,
∵AB=BC,
∴
BD2=AD2+BD2-
AD•BD,
整理得:3AD2+BD2-4AD•BD=0,
因式分解:(BD-3AD)(BD-AD)=0,
∵DA≠DB,
∴BD=3AD,
∴
=
.
∴∠DAE=∠DCB,
∴∠DAE=∠DAC,∠DAC=∠DBC,
∴∠DCB=∠DBC,
∴BD=CD,
∵AB=BC,
∴∠ADB=∠FDC,
∵∠DAB=∠DAC+∠BAC,∠DFC=∠DBC+∠BCA,∠BCA=∠BAC,
∴∠DAB=∠DFC,
在△DAB和△DFC中,
|
∴△DAB≌△DFC(AAS);
(2)解:∵∠BAC=∠BDC,∠ADB=∠BDC,
∴∠BDC=∠BAC,
∵在△BDC中有BC2=BD2+CD2-2BD•CD•cos∠BDC,
∴整理得:BC2=
| 2 |
| 3 |
∵△ADB中,AB2=AD2+BD2-2AD•BDcos∠ADB,
∴整理得:AB2=AD2+BD2-
| 4 |
| 3 |
∵AB=BC,
∴
| 2 |
| 3 |
| 4 |
| 3 |
整理得:3AD2+BD2-4AD•BD=0,
因式分解:(BD-3AD)(BD-AD)=0,
∵DA≠DB,
∴BD=3AD,
∴
| DA |
| DB |
| 1 |
| 3 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△DAB≌△DFC是解题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
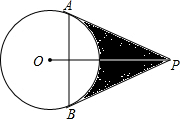 如图,已知PA,PB切⊙O于A、B两点,连AB,∠APB=60°AB=
如图,已知PA,PB切⊙O于A、B两点,连AB,∠APB=60°AB=
 如图,以O为顶点的两条抛物线分别经过正方形的四个顶点A、B、C、D,则阴影部分的面积为
如图,以O为顶点的两条抛物线分别经过正方形的四个顶点A、B、C、D,则阴影部分的面积为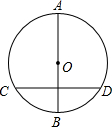 如图,在⊙O中AB为直径,CD为非直径的弦,(1)AB⊥CD;(2)AB平分CD;(3)AB平分CD所对的两条弧.若以(1)、(2)、(3)中的一个为条件,另两个为结论构成三个命题,其中真命题的个数为( )
如图,在⊙O中AB为直径,CD为非直径的弦,(1)AB⊥CD;(2)AB平分CD;(3)AB平分CD所对的两条弧.若以(1)、(2)、(3)中的一个为条件,另两个为结论构成三个命题,其中真命题的个数为( )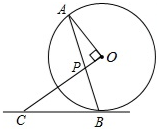 如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P.
如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P. △ABC中,AB=AC,AD⊥BC于D,以AC为边在△ABC外作等边△ACE,连BE交AD于M;
△ABC中,AB=AC,AD⊥BC于D,以AC为边在△ABC外作等边△ACE,连BE交AD于M; 如图,在一个矩形纸片ABCD剪上减去一个正方形ABEF,所余下的矩形ECDF于原矩形ABCD相似,那么原矩形中较长的边BC与较短的边AB的比是多少?
如图,在一个矩形纸片ABCD剪上减去一个正方形ABEF,所余下的矩形ECDF于原矩形ABCD相似,那么原矩形中较长的边BC与较短的边AB的比是多少?