题目内容
7.已知二次函数y=ax2+bx+c(a≠0)的图象经过A(0,0),B(2,0)两点,请你写出一组满足条件的实数a,b的对值:a=1,b=-2.分析 把A点和B点坐标代入y=ax2+bx+c可求出c的值,得到a和b的关系式,然后当a取不为0的一个值时,计算出对应的b的值即可.
解答 解:把A(0,0),B(2,0)代入y=ax2+bx+c得$\left\{\begin{array}{l}{c=0}\\{4a+2b+c=0}\end{array}\right.$,
所以2a+b=0,c=0,
当a=1时,b=-2.
故答案为1,-2.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
15.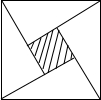 2002年8月在北京召开的国际数学家大会会标,它是有四个全等的小正方形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会标,它是有四个全等的小正方形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )
 2002年8月在北京召开的国际数学家大会会标,它是有四个全等的小正方形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会标,它是有四个全等的小正方形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )| A. | 13 | B. | 19 | C. | 25 | D. | 169 |
12.在直角坐标系中,点M($\sqrt{3}$,-2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.已知y=x2-x-1,则其图象的开口方向及顶点坐标分别是( )
| A. | 开口向上,顶点($\frac{1}{2}$,-$\frac{5}{4}$) | B. | 开口向下,顶点($\frac{1}{2}$,-$\frac{5}{4}$) | ||
| C. | 开口向上,顶点(-$\frac{1}{2}$,$\frac{5}{4}$) | D. | 开口向下,顶点(-$\frac{1}{2}$,$\frac{5}{4}$) |
 如图,⊙O的直径CD⊥AB,∠A=30°,则∠D=30°.
如图,⊙O的直径CD⊥AB,∠A=30°,则∠D=30°.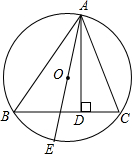 如图,△ABC是⊙O的内接三角形,AD⊥BC于点D,AE是⊙O的直径,若S△ABC=S,⊙O的半径为R.求证:
如图,△ABC是⊙O的内接三角形,AD⊥BC于点D,AE是⊙O的直径,若S△ABC=S,⊙O的半径为R.求证: