题目内容
19.已知y=x2-x-1,则其图象的开口方向及顶点坐标分别是( )| A. | 开口向上,顶点($\frac{1}{2}$,-$\frac{5}{4}$) | B. | 开口向下,顶点($\frac{1}{2}$,-$\frac{5}{4}$) | ||
| C. | 开口向上,顶点(-$\frac{1}{2}$,$\frac{5}{4}$) | D. | 开口向下,顶点(-$\frac{1}{2}$,$\frac{5}{4}$) |
分析 将二次函数配方成顶点式即可确定其顶点坐标,开口方向有二次项系数的符号决定.
解答 解:∵y=x2-x-1=(x-$\frac{1}{2}$)2-$\frac{5}{4}$,
∴顶点坐标为:($\frac{1}{2}$,-$\frac{5}{4}$),
∵a=1>0,
∴开口方向向上,
故选A.
点评 本题考查了二次函数的性质,解题的关键是能够将二次函数配方成顶点式,也可以采用顶点坐标公式求解.

练习册系列答案
相关题目
14.下列说法正确的是( )
| A. | (3,2)和(2,3)表示一个点 | B. | 点($\sqrt{3}$,0)在x轴的正半轴上 | ||
| C. | 点(-2,4)在第四象限 | D. | 点(3,-1)到x轴的距离为3 |
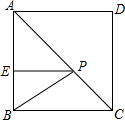 如图,正方形ABCD的边长为3,AE=2BE,P是AC上一动点,则PB+PE的最小值为$\sqrt{13}$.
如图,正方形ABCD的边长为3,AE=2BE,P是AC上一动点,则PB+PE的最小值为$\sqrt{13}$.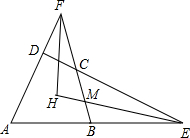 如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.
如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.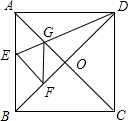 如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:①∠AGD=112.5°;②AD=2AE;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的序号是( )
如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:①∠AGD=112.5°;②AD=2AE;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的序号是( )