题目内容
15.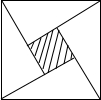 2002年8月在北京召开的国际数学家大会会标,它是有四个全等的小正方形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会标,它是有四个全等的小正方形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )| A. | 13 | B. | 19 | C. | 25 | D. | 169 |
分析 根据勾股定理可以求得a2+b2等于大正方形的面积,然后求四个直角三角形的面积,即可得到ab的值,然后根据(a+b)2=a2+2ab+b2即可求解.
解答 解:根据勾股定理可得a2+b2=13,
四个直角三角形的面积是:$\frac{1}{2}$ab×4=13-1=12,即:2ab=12
则(a+b)2=a2+2ab+b2=13+12=25.
故选C.
点评 本题考查勾股定理,以及完全平方式,正确根据图形的关系求得a2+b2和ab的值是关键.

练习册系列答案
相关题目
5.下列说法正确的是( )
| A. | 有且只有一条直线垂直于已知直线 | |
| B. | 互相垂直的直线一定相交 | |
| C. | 从直线外一点到这条直线的垂线段叫做点到直线的距离 | |
| D. | 直线L外一点P与直线L上各点连接而成的线段中最短线段的长度是3cm,则点P到直线L的距离是3cm. |
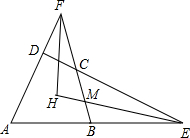 如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.
如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.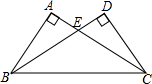 如图,∠BAC=90°,∠EDC=90°,∠DCE=30°,ED=2,AB=3,求S△CEB的值.
如图,∠BAC=90°,∠EDC=90°,∠DCE=30°,ED=2,AB=3,求S△CEB的值.