题目内容
17．求直线11：2x+y-4=0关于直线l：3x+4y-1=0对称的直线l2的方程．分析 使用到角公式求所求直线斜率，求得结果．
解答 解：由
2x+y-4=0，
3x+4y-1=0，
设直线b的斜率为k，又知直线a的斜率为-2，直线l的斜率为-$\frac{3}{4}$．
则$\frac{-\frac{3}{4}-（-2）}{1+（-\frac{3}{4}）×（-2）}=\frac{k-（-\frac{3}{4}）}{1+k（-\frac{3}{4}）}$．
解得k=-$\frac{2}{11}$．
代入点斜式得直线b的方程为
y-（-2）=-$\frac{2}{11}$（x-3），
即2x+11y+16=0．
点评 本题考查直线关于直线对称问题，关键是使用到角公式求所求直线斜率解答．
练习册系列答案
名校课堂系列答案
相关题目
7．
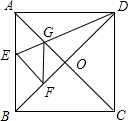如图，在正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，A恰好与BD上的点F重合，展开后，折痕DE分别交AB，AC于点E、G，连接GF，有下列结论：①∠AGD=112.5°；②AD=2AE；③S△AGD=S△OGD；④四边形AEFG是菱形；⑤BE=2OG．其中正确结论的序号是（ ）
如图，在正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，A恰好与BD上的点F重合，展开后，折痕DE分别交AB，AC于点E、G，连接GF，有下列结论：①∠AGD=112.5°；②AD=2AE；③S△AGD=S△OGD；④四边形AEFG是菱形；⑤BE=2OG．其中正确结论的序号是（ ）| A． | ①②③ | B． | ①③④ | C． | ①④⑤ | D． | ①②③④⑤ |
4．某工程甲单独做x天完成，乙单独做比甲慢3天完成，现由甲、乙合作5天后，余下的工程由甲单独做3天才能全部完成，则下列方程中符合题意的是（ ）
| A． | $\frac{8}{x}+\frac{5}{x-3}=1$ | B． | $（\frac{1}{x}+\frac{1}{x+3}）×5+\frac{3}{x}=1$ | C． | $\frac{3}{x-3}+5（\frac{1}{x-3}+\frac{1}{x}）=1$ | D． | $\frac{5}{x+（x+3）}+\frac{3}{x}=1$ |
5．
如图，直线a∥b，∠1=120°，则∠2的度数是（ ）
如图，直线a∥b，∠1=120°，则∠2的度数是（ ）| A． | 120° | B． | 80° | C． | 60° | D． | 50° |