题目内容
2.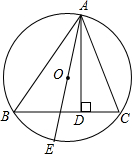 如图,△ABC是⊙O的内接三角形,AD⊥BC于点D,AE是⊙O的直径,若S△ABC=S,⊙O的半径为R.求证:
如图,△ABC是⊙O的内接三角形,AD⊥BC于点D,AE是⊙O的直径,若S△ABC=S,⊙O的半径为R.求证:(1)AB•AC=AD•AE;
(2)AB•AC•BC=4RS.
分析 (1)首先连接BE,由AD是⊙O的内接△ABC的高,AE是⊙O的直径,可得∠ABE=∠ADC=90°,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,可得∠E=∠C,即可证得△ABE∽△ADC,然后由相似三角形的对应边成比例,证得AB•AC=AD•AE;
(2)由于S△ABC=S=$\frac{1}{2}$BC•AD,推出BC=$\frac{2S}{AD}$,根据AE=2R,AB•AC=AD•AE,代入AB•AC•BC,即可得到结论.
解答 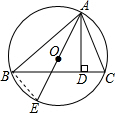 证明:(1)连接BE,
证明:(1)连接BE,
∵AD是⊙O的内接△ABC的高,AE是⊙O的直径,
∴∠ABE=∠ADC=90°,
∵∠E=∠C,
∴△ABE∽△ADC,
∴AB:AD=AE:AC,
∴AB•AC=AD•AE;
(2)∵S△ABC=S=$\frac{1}{2}$BC•AD,
∴BC=$\frac{2S}{AD}$,
∵AE=2R,AB•AC=AD•AE,
∴AB•AC•BC=AD•AE•BC=AD•2R•$\frac{2S}{AD}$=4RS.
点评 此题考查了相似三角形的判定与性质以及圆周角定理,三角形面积公式,连接BE构造直角三角形是解题的关键.

练习册系列答案
相关题目
14.下列说法正确的是( )
| A. | (3,2)和(2,3)表示一个点 | B. | 点($\sqrt{3}$,0)在x轴的正半轴上 | ||
| C. | 点(-2,4)在第四象限 | D. | 点(3,-1)到x轴的距离为3 |
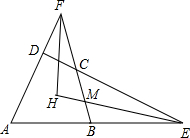 如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.
如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.