题目内容
18.读一读:式子“1+2+3+4+…+100”表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为$\sum_{n=1}^{100}$n,这里“∑”是求和符号,通过对以上材料的阅读,计算$\sum_{n=1}^{2016}$$\frac{1}{n(n+1)}$=$\frac{2016}{2017}$.分析 根据定义,将$\sum_{n=1}^{2016}$$\frac{1}{n(n+1)}$写成$\frac{1}{1×2}+\frac{1}{2×3}+…+\frac{1}{2016×2017}$后运用$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$化简计算可得结果.
解答 解:根据题意,知:
$\sum_{n=1}^{2016}$$\frac{1}{n(n+1)}$=$\frac{1}{1×2}+\frac{1}{2×3}+…+\frac{1}{2016×2017}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2016}$-$\frac{1}{2017}$
=1-$\frac{1}{2017}$
=$\frac{2016}{2017}$,
故答案为:$\frac{2016}{2017}$
点评 本题主要考查新定义下分式的化简计算,根据对定义的理解准确列出算式是解题的前提,运用公式将分数拆开运算是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.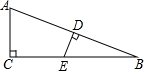 如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )
如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )
 如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )
如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )| A. | $\frac{12}{5}$ | B. | $\frac{13}{5}$ | C. | $\frac{169}{24}$ | D. | $\frac{60}{13}$ |
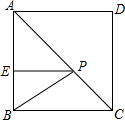 如图,正方形ABCD的边长为3,AE=2BE,P是AC上一动点,则PB+PE的最小值为$\sqrt{13}$.
如图,正方形ABCD的边长为3,AE=2BE,P是AC上一动点,则PB+PE的最小值为$\sqrt{13}$.
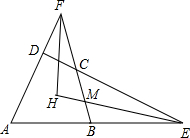 如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.
如图,四边形ABCD中,∠BAD+∠BCD=180°,AD,BC的延长线交于点F,DC,AB的延长线交于点E,∠E,∠F的平分线交于点H.求证:EH⊥FH.