题目内容
4.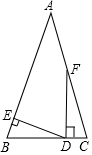 如图,在△ABC中,AB=AC,点D在边BC上,DE⊥AB于点E,DF⊥BC交AC于点F.若∠EDF=70°,则∠AFD等于160°.
如图,在△ABC中,AB=AC,点D在边BC上,DE⊥AB于点E,DF⊥BC交AC于点F.若∠EDF=70°,则∠AFD等于160°.
分析 由DF⊥BC有∠FDB=90°,而∠EDF=70°,根据三角形内角和定理得到∠BDE=90°-70°=20°,由DE⊥AB得到∠DEB=90°,根据三角形内角和定理得到求出∠B的度数和∠C的度数,进而求出∠CFD的度数,利用邻补角的知识求出∠AFD的度数.
解答 解:∵DF⊥BC,
∴∠FDB=90°,
而∠EDF=70°,
∴∠BDE=90°-70°=20°,
∵DE⊥AB,
∴∠DEB=90°,
∴∠B=180°-∠DEB-∠BDE=180°-90°-20°=70°,
∴∠C=∠B=70°,
∴∠CFD=90°-70°=20°,
∴∠AFD=180°-20°=160°.
故答案为160°.
点评 本题主要考查了等腰三角形的性质以及三角形内角和的知识,解题的关键是求出∠B和∠C的度数,此题难度不大.

练习册系列答案
相关题目
13.在菱形ABCD中,AC,BD为对角线,下列说法一定正确的是( )
| A. | AC=BD | B. | AC⊥BD | C. | ∠ABD=∠BAC | D. | ∠BAC+∠CAD=90° |
14.已知关于x 的分式方程$\frac{a+2}{x+1}$=1的解是非正数,则a的取值范围是( )
| A. | a≤-1且a≠-2 | B. | a≤-1 | C. | a≤1且a≠-2 | D. | a≤1 |
 如图,?ABCD中,E、F在AC上,四边形DEBF是平行四边形,求证:AE=CF.
如图,?ABCD中,E、F在AC上,四边形DEBF是平行四边形,求证:AE=CF. 在△ABC中,AB=AC=10,∠A=36°,BD平分∠ABC,求AD、DC的长.
在△ABC中,AB=AC=10,∠A=36°,BD平分∠ABC,求AD、DC的长.
 如图放置的正方形ABCD,正方形DCC1D1,正方形D1C1C2D2,…都是边长为$\sqrt{3}$的正方形,点A在y轴上,点B,C,C1,C2,…,都在直线y=$\frac{\sqrt{3}}{3}$x上,则D的坐标是($\sqrt{3}$,1+$\frac{4\sqrt{3}}{3}$),Dn的坐标是($\sqrt{3}$(n+1),$\frac{3(n+1)+4\sqrt{3}}{3}$).
如图放置的正方形ABCD,正方形DCC1D1,正方形D1C1C2D2,…都是边长为$\sqrt{3}$的正方形,点A在y轴上,点B,C,C1,C2,…,都在直线y=$\frac{\sqrt{3}}{3}$x上,则D的坐标是($\sqrt{3}$,1+$\frac{4\sqrt{3}}{3}$),Dn的坐标是($\sqrt{3}$(n+1),$\frac{3(n+1)+4\sqrt{3}}{3}$). 如图,△ABC中,AB=AC,D为BC上一点,CD=DE,证明:A、B、D、E四点共圆.
如图,△ABC中,AB=AC,D为BC上一点,CD=DE,证明:A、B、D、E四点共圆.