题目内容
15. 在△ABC中,AB=AC=10,∠A=36°,BD平分∠ABC,求AD、DC的长.
在△ABC中,AB=AC=10,∠A=36°,BD平分∠ABC,求AD、DC的长.
分析 由在△ABC中,AB=AC=10,∠A=36°,BD平分∠ABC,易证得AD=BD=BC,△CBD∽△BAC,设AD=x,则DC=10-x,然后由相似三角形的对应边成比例,即可求得AD、DC的长.
解答 解:设AD=x,则DC=AC-AD=10-x.
∵在△ABC中,AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
∴∠ABD=∠CDB=36°,
∴∠A=∠ABD,∠BDC=∠A+∠ABD=72°=∠C,
∴AD=BD=BC=x,
∵∠DBC=∠A,∠C=∠C,
∴△DBC∽△BAC,
∴$\frac{BD}{AB}$=$\frac{CD}{BC}$,
即$\frac{x}{10}$=$\frac{10-x}{x}$,
解得:x=-5+5$\sqrt{5}$或x=-5-5$\sqrt{5}$(舍去),
∴AD=-5+5$\sqrt{5}$,DC=10-(-5+5$\sqrt{5}$)=15-5$\sqrt{5}$.
点评 此题考查了相似三角形的判定与性质以及等腰三角形的判定与性质.此题难度适中,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
10. 如图,在△ABC中,AB=AC,点D在边BC上,根据等腰三角形″三线合一″的性质填写结论:
如图,在△ABC中,AB=AC,点D在边BC上,根据等腰三角形″三线合一″的性质填写结论:
①若BD=CD,则AD⊥BC.
②AD⊥BC,垂足为D,则BD=CD.
③若AD平分∠BAC,则AD⊥BC.
 如图,在△ABC中,AB=AC,点D在边BC上,根据等腰三角形″三线合一″的性质填写结论:
如图,在△ABC中,AB=AC,点D在边BC上,根据等腰三角形″三线合一″的性质填写结论:①若BD=CD,则AD⊥BC.
②AD⊥BC,垂足为D,则BD=CD.
③若AD平分∠BAC,则AD⊥BC.
7.甲、乙、丙、丁,四名学生在判断钟表的分针和时针互相垂直的时刻时,每人说了两个时刻,说法都对的是( )
| A. | 甲:“3时整和3时30分” | B. | 乙说“6时15分和6时45分” | ||
| C. | 丙说“9时整和12时15分” | D. | 丁说:“3时整和9时整” |
 已知:如图所示,在四边形ABCD中,E、F分别为AB、CD的中点
已知:如图所示,在四边形ABCD中,E、F分别为AB、CD的中点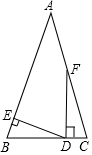 如图,在△ABC中,AB=AC,点D在边BC上,DE⊥AB于点E,DF⊥BC交AC于点F.若∠EDF=70°,则∠AFD等于160°.
如图,在△ABC中,AB=AC,点D在边BC上,DE⊥AB于点E,DF⊥BC交AC于点F.若∠EDF=70°,则∠AFD等于160°.