题目内容
3. 如图,AB为⊙O的直径,点P是⊙O外一点,PD与⊙O相切于点C,与BA的延长线交于点D,DE⊥PO,交PO的延长线于点E,连接PB,∠EDB=∠EPB.
如图,AB为⊙O的直径,点P是⊙O外一点,PD与⊙O相切于点C,与BA的延长线交于点D,DE⊥PO,交PO的延长线于点E,连接PB,∠EDB=∠EPB.(1)求证:PB是⊙O的切线;
(2)若PB=3,DB=4,求⊙O的半径.
分析 (1)根据题意可以求得∠DEO=∠PBO,再根据PE⊥DE,从而可以解答本题;
(2)根据切线的性质和勾股定理可以求得⊙O的半径.
解答 (1)证明:∵∠EDB=∠EPB,∠DOE=∠POB,
∴∠DEO=∠PBO,
∵DE⊥PE,
∴∠DEO=90°,
∴∠PBO=90°,
∴PB是⊙O的切线;
(2)由(1)知,PB是⊙O的切线,
∴∠PBD=90°,
∵PB=3,DB=4,
∴PD=5,
∵PC和PB都是⊙O的切线,
∴PC=PB=3,∠OCD=90°,
∴CD=2,
设⊙O的半径为x,则OC=x,OD=4-x,
则22+x2=(4-x)2,
解得,x=$\frac{3}{2}$,
即⊙O的半径是$\frac{3}{2}$.
点评 本题考查切线的性质与判定,解答本题的关键是明确题意,找出所求问题需要的条件,利用切线的性质和勾股定理解答.

练习册系列答案
相关题目
13.已知△ABC∽△DEF,若△ABC与△DEF的相似比为2:3,则△ABC与△DEF对应边上的中线的比为( )
| A. | 2:3 | B. | 4:16 | C. | 3:2 | D. | 16:4 |
14.在△ABC中,∠C=90°,BC=3,AB=5,点D在△ABC的边上,且AD=1,将△ABC折叠,使点B落在点D处,折痕交边AB于点E,交另一边于点F,则BE=2或$\frac{15}{7}$.
11.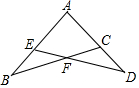 如图,△ABC、△ADE中,C、E两点分别在AD、AB上,且BC与DE相交于F点,若∠A=90°,∠B=∠D=30°,AC=AE=1,则四边形AEFC的周长为何( )
如图,△ABC、△ADE中,C、E两点分别在AD、AB上,且BC与DE相交于F点,若∠A=90°,∠B=∠D=30°,AC=AE=1,则四边形AEFC的周长为何( )
 如图,△ABC、△ADE中,C、E两点分别在AD、AB上,且BC与DE相交于F点,若∠A=90°,∠B=∠D=30°,AC=AE=1,则四边形AEFC的周长为何( )
如图,△ABC、△ADE中,C、E两点分别在AD、AB上,且BC与DE相交于F点,若∠A=90°,∠B=∠D=30°,AC=AE=1,则四边形AEFC的周长为何( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 2+$\sqrt{2}$ | D. | 2+$\sqrt{3}$ |
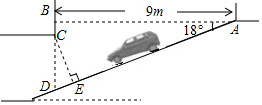 为缓解“停车难”的问题,某单位拟造地下停车库,建筑设计师提供了该地下停车库的设计示意图如图所示,已知该坡道的水平距离AB的长为9m,坡面AD与AB的夹角∠BAD=18°,石柱BC=0.5m,按规定,地下停车库坡道上方BC处要张贴限高标志,以便告知停车人车辆能否安全驶入.请你帮设计师计算一下CE的高度,以便张贴限高标志,结果精确到0.1m.
为缓解“停车难”的问题,某单位拟造地下停车库,建筑设计师提供了该地下停车库的设计示意图如图所示,已知该坡道的水平距离AB的长为9m,坡面AD与AB的夹角∠BAD=18°,石柱BC=0.5m,按规定,地下停车库坡道上方BC处要张贴限高标志,以便告知停车人车辆能否安全驶入.请你帮设计师计算一下CE的高度,以便张贴限高标志,结果精确到0.1m.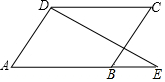 如图,AD∥BC,∠CDE=∠E,试判断∠A与∠C之间的关系,并说明理由.
如图,AD∥BC,∠CDE=∠E,试判断∠A与∠C之间的关系,并说明理由.