题目内容
13.已知△ABC∽△DEF,若△ABC与△DEF的相似比为2:3,则△ABC与△DEF对应边上的中线的比为( )| A. | 2:3 | B. | 4:16 | C. | 3:2 | D. | 16:4 |
分析 相似三角形对应边上中线的比等于相似比,根据以上性质得出即可.
解答 解:∵△ABC∽△DEF,△ABC与△DEF的相似比为2:3,
∴△ABC与△DEF对应边上中线的比是2:3,
故选A.
点评 本题考查了相似三角形的性质的应用,能理解相似三角形的性质是解此题的关键,注意:相似三角形对应边上中线的比等于相似比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8. 如图,在△ABC中,AB=AC=13,BC=24,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )
如图,在△ABC中,AB=AC=13,BC=24,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )
 如图,在△ABC中,AB=AC=13,BC=24,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )
如图,在△ABC中,AB=AC=13,BC=24,D是线段BC上的动点(不含端点B,C),若线段AD长为正整数,则点D的个数共有( )| A. | 15个 | B. | 14个 | C. | 13个 | D. | 12个 |
2.在一个不透明袋子中装有5个红球、3个绿球,这些球除了颜色外无其他差别,从袋子中随机摸出一个球,摸出红球的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
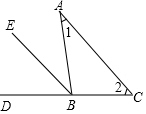 如图,已知在△ABC中,∠1=∠2.
如图,已知在△ABC中,∠1=∠2.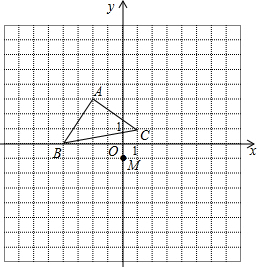 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,3),B(-4,0),C(1,1).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,3),B(-4,0),C(1,1). 如图,AB为⊙O的直径,点P是⊙O外一点,PD与⊙O相切于点C,与BA的延长线交于点D,DE⊥PO,交PO的延长线于点E,连接PB,∠EDB=∠EPB.
如图,AB为⊙O的直径,点P是⊙O外一点,PD与⊙O相切于点C,与BA的延长线交于点D,DE⊥PO,交PO的延长线于点E,连接PB,∠EDB=∠EPB.