题目内容
11.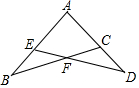 如图,△ABC、△ADE中,C、E两点分别在AD、AB上,且BC与DE相交于F点,若∠A=90°,∠B=∠D=30°,AC=AE=1,则四边形AEFC的周长为何( )
如图,△ABC、△ADE中,C、E两点分别在AD、AB上,且BC与DE相交于F点,若∠A=90°,∠B=∠D=30°,AC=AE=1,则四边形AEFC的周长为何( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 2+$\sqrt{2}$ | D. | 2+$\sqrt{3}$ |
分析 根据三角形的内角和得到∠AED=∠ACB=60°,根据三角形的外角的性质得到∠B=∠EFB=∠CFD=∠D,根据等腰三角形的判定得到BE=EF=CF=CD,于是得到四边形AEFC的周长=AB+AC.
解答 解:∵∠A=90°,∠B=∠D=30°,
∴∠AED=∠ACB=60°,
∵∠AED=∠B+∠EFB=∠ACB=∠CFD+∠D=60°,
∴∠EFB=∠CFD=30°,
∴∠B=∠EFB=∠CFD=∠D,
∴BE=EF=CF=CD,
∴四边形AEFC的周长=AB+AC,
∵∠A=90°,AE=AC=1,
∴AB=AD=$\sqrt{3}$,
∴四边形AEFC的周长=2$\sqrt{3}$.
故选B.
点评 本题考查了等腰三角形的性质,解直角三角形,三角形的外角的性质,熟练掌握等腰三角形的判定与性质是解题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
2.在一个不透明袋子中装有5个红球、3个绿球,这些球除了颜色外无其他差别,从袋子中随机摸出一个球,摸出红球的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
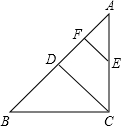 如图,Rt△ABC中,∠ACB=90°,AB=6,点D是AB的中点,过AC的中点E作EF∥CD交AB于点F,则EF=1.5.
如图,Rt△ABC中,∠ACB=90°,AB=6,点D是AB的中点,过AC的中点E作EF∥CD交AB于点F,则EF=1.5. 如图,AB为⊙O的直径,点P是⊙O外一点,PD与⊙O相切于点C,与BA的延长线交于点D,DE⊥PO,交PO的延长线于点E,连接PB,∠EDB=∠EPB.
如图,AB为⊙O的直径,点P是⊙O外一点,PD与⊙O相切于点C,与BA的延长线交于点D,DE⊥PO,交PO的延长线于点E,连接PB,∠EDB=∠EPB. 实践操作
实践操作