题目内容
3.如图,抛物线y=ax2+bx+c与x轴交于点A(-2,0)和点B(6,0),与y轴交于点C(0,3),点D是抛物线上的点,且CD∥x轴,点E是抛物线的顶点.(1)求抛物线的解析式;
(2)平移该抛物线的对称轴所在直线L,当L平移到何处时,恰好将△BCD的面积分为相等的两部分?
(3)点F在线段CD上,若以点C,E,F为顶点的三角形与△COE相似,试求点F的坐标.
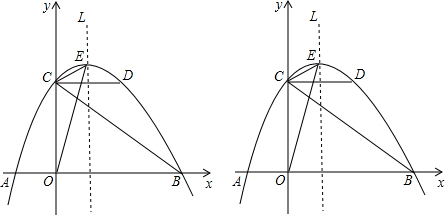
分析 (1)利用待定系数法即可求得抛物线的解析式;
(2)首先求得D的坐标,则CD的长即可求得,进而求得△BCD的面积,当l平移至l1,l1与CD、BC分别交于点M、N,易证△CMN∽△BOC,求得CM和MN的关系,利用三角形的面积公式即可求解;
(3)分成△COE∽△ECF和△COE∽△FCE两种情况,利用相似三角形的对应边的比相等即可求解.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{4a-2b+c=0}\\{36a+6b+c=0}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=1}\\{c=3}\end{array}\right.$.
则抛物线的解析式是y=-$\frac{1}{4}$x2+x+3;
(2)抛物线y=-$\frac{1}{4}$x2+x+3的对称轴是x=2.
∵CD∥x轴,C的坐标是(0,3),
∴D的坐标是(4,3),
∴S△BCD=$\frac{1}{2}$CD•OC=$\frac{1}{2}$×4×3=6.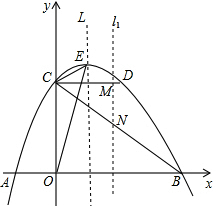
如图,当l平移至l1,l1与CD、BC分别交于点M、N.
∴∠MCN=∠CBO,∠CMN=∠BOC=90°,
∴△CMN∽△BOC,
∴$\frac{CM}{MN}$=$\frac{BO}{OC}$=$\frac{6}{3}$=2,
∴CM=2MN,
∴S△CMN=$\frac{1}{2}$CM•MN=$\frac{1}{4}$CM2.
∵S△CMN=$\frac{1}{2}$S△BCD,
∴$\frac{1}{4}$CM2=3,
∴CM=2$\sqrt{3}$.
∴当l平移到直线x=2$\sqrt{3}$处时,恰好将△BCD的面积分成面积相等的两部分;
(3)设对称轴l交CD于点P,过点E作EQ⊥y轴,垂足为点Q.
∵E(2,4),C(0,3),CD∥x轴,
∴$\frac{EQ}{OQ}$=$\frac{EP}{CP}$=$\frac{1}{2}$,
又∵∠EQO=∠EPC=90°,
∴△EQC∽△EPC,
∴∠COE=∠ECD.
∵C(0,3),E(2,4),
∴CE=$\sqrt{5}$,OE=2$\sqrt{5}$.
分成两种情况:
当△COE∽△ECF是,$\frac{CO}{CE}$=$\frac{OE}{CF}$,
∴CF=$\frac{10}{3}$,
∴F的坐标是($\frac{10}{3}$,3);
当△COE∽△FCE时,$\frac{CO}{CF}$=$\frac{OE}{CE}$,
∴CF=$\frac{3}{2}$.
∴F的坐标是($\frac{3}{2}$,3).
则满足条件的F的坐标是($\frac{10}{3}$,3)或($\frac{3}{2}$,3).
点评 本题考查了待定系数法求函数的解析式以及相似三角形的判定与性质,正确分成△COE∽△ECF和△COE∽△FCE两种情况进行讨论是关键.

| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
| A. | y=8x2+1 | B. | y=2x-3 | C. | y=3x2+$\frac{1}{{x}^{2}}$ |
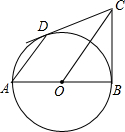 如图,已知AB为⊙O的直径,CB、CD分别切⊙O于点B、D.求证:AD∥OC.
如图,已知AB为⊙O的直径,CB、CD分别切⊙O于点B、D.求证:AD∥OC.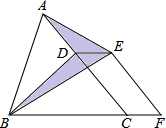 如图,已知△ABC的面积为36,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
如图,已知△ABC的面积为36,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )