题目内容
13.当-1≤x≤1时,函数y=-x2-2mx+2n+1的最小值是-4,最大值是0,求m、n的值.分析 首先将二次函数配方确定其对称轴,然后根据m的取值分类讨论即可确定m、n的值.
解答 解:y=-x2-2mx+2n+1=-(x+m)2+m2+2n+1,其对称轴为直线x=-m,
①当-m≤-1,即m≥1时,$\left\{{\begin{array}{l}{-1-2m+2n+1=-4}\\{-1+2m+2n+1=0}\end{array}}\right.$,
解得$\left\{{\begin{array}{l}{m=1}\\{n=-1}\end{array}}\right.$,
②当-1<-m<0,即0<m<1时,$\left\{{\begin{array}{l}{{m^2}+2n+1=0}\\{-1-2m+2n+1=-4}\end{array}}\right.$,
消去n得,m2+2m-3=0,
解得m=1或m=-3,舍去;
③当 0<-m<1,即-1<m<0时,$\left\{{\begin{array}{l}{{m^2}+2n+1=0}\\{-1+2m+2n+1=-4}\end{array}}\right.$
解得m=-1或m=3,舍去;
④当-m≥1,即m≤-1时,$\left\{{\begin{array}{l}{-1-2m+2n+1=0}\\{-1+2m+2n+1=-4}\end{array}}\right.$,
解得$\left\{{\begin{array}{l}{m=-1}\\{n=-1}\end{array}}\right.$,
综上所述m=1,n=-1或m=-1,n=-1.
点评 本题考查了二次函数的最值,本题主要考查x取值范围的讨论,比较复杂,有一定难度.

练习册系列答案
相关题目
2.若实数a,b满足a2+3a=2,b2+3b=2,且a≠b,则(1+a2)(1+b2)=( )
| A. | 18 | B. | 12 | C. | 9 | D. | 6 |
 如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数50°.
如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数50°.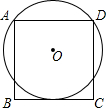 如图,已知⊙O过正方形ABCD的顶点A、D,且与BC边相切,若⊙O的半径为1,则正方形的边长为$\frac{8}{5}$.
如图,已知⊙O过正方形ABCD的顶点A、D,且与BC边相切,若⊙O的半径为1,则正方形的边长为$\frac{8}{5}$.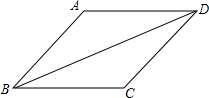 如图,菱形ABCD的边长为5,sin∠ABC=$\frac{4}{5}$,则对角线BD的长为4$\sqrt{5}$.
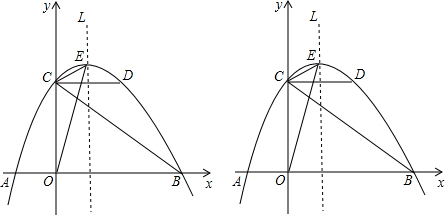
如图,菱形ABCD的边长为5,sin∠ABC=$\frac{4}{5}$,则对角线BD的长为4$\sqrt{5}$. 如图,在平面直角坐标系中,⊙D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.
如图,在平面直角坐标系中,⊙D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.