题目内容
12.某情报站有A,B,C,D四种互不相同的密码,每周使用其中的一种密码,且每周都是从上周未使用的三种密码中等可能地随机选用一种.设第1周使用A种密码,那么第7周也使用A种密码的概率是$\frac{61}{243}$.分析 由题意可得,第n+1周也使用A种密码的概率 Pn+1=Pn•$\frac{1}{3}$,且P2=0,P3=$\frac{1}{3}$,以此类推可得第七周使用A的概率P7 的值.
解答 解:第一周使用A,第二周使用A的概率P2=0,第三周使用A的概率P3=$\frac{1}{3}$,依此类推,
第四周使用A的概率 P4=(1-$\frac{1}{3}$)•$\frac{1}{3}$=$\frac{2}{9}$,
第五周使用A的概率P5=(1-$\frac{2}{9}$)•$\frac{1}{3}$=$\frac{7}{27}$,
第六周使用A的概率P6=(1-P5)•$\frac{1}{3}$=$\frac{20}{81}$,
第七周使用A的概率P7=(1-P6)•$\frac{1}{3}$=$\frac{61}{243}$;
故答案为:$\frac{61}{243}$.
点评 此题主要考查了概率公式,得到第n+1周也使用A种密码的概率 Pn+1=Pn•$\frac{1}{3}$,是解题的关键,属于中档题.

练习册系列答案
相关题目
16.某校九年级共有450名学生,为了了解该年级学生的数学解题能力情况,该校数学兴趣小组随机抽取了90人进行调查分析,并将抽取的学生的数学解题成绩进行分组,绘制如下频数分布表和成绩分布扇形统计图(图1):
该校90名学生数学解题成绩频数分布表
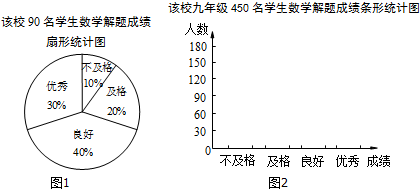
(1)根据抽样调查的结果,将估计出该校九年级450名学生数学解题成绩情况在图2中绘制成条形统计图:
(2)请你结合上述统计的结果,提出一条合理化建议.
该校90名学生数学解题成绩频数分布表
| 成绩 | 划记 | 频数 |
| 不及格 | 正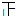 | 9 |
| 及格 | 正正正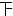 | 18 |
| 良好 | 正正正正正正一 | 36 |
| 优秀 | 正正正正正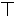 | 27 |
| 合计 | 90 |

(1)根据抽样调查的结果,将估计出该校九年级450名学生数学解题成绩情况在图2中绘制成条形统计图:
(2)请你结合上述统计的结果,提出一条合理化建议.
2.若实数a,b满足a2+3a=2,b2+3b=2,且a≠b,则(1+a2)(1+b2)=( )
| A. | 18 | B. | 12 | C. | 9 | D. | 6 |
 如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数50°.
如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数50°.