题目内容
11．
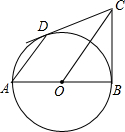如图，已知AB为⊙O的直径，CB、CD分别切⊙O于点B、D．求证：AD∥OC．
分析 连接OD，根据切线的性质可知CD=CB，根据SSS定理得出△OBC≌△ODC，故可得出∠BOC=∠DOC，根据圆心角、弧的关系可得出$\widehat{DE}$=$\widehat{BE}$，再由圆周角定理可知∠BOC=∠A，故可得出结论．
解答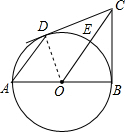 
证明：连接OD，
∵CB、CD分别切⊙O于点B、D，
∴CD=CB．
在△OBC与△ODC中，
∵$\left\{\begin{array}{l}OC=OC\\ OD=OB\\ CD=CB\end{array}\right.$
∴△OBC≌△ODC（SSS），
∴∠BOC=∠DOC，
∴$\widehat{DE}$=$\widehat{BE}$，
∴∠BOC=∠A，
∴AD∥OC．
点评 本题考查的是切线的性质，根据题意作出辅助线，构造出全等三角形是解答此题的关键．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
16．某校九年级共有450名学生，为了了解该年级学生的数学解题能力情况，该校数学兴趣小组随机抽取了90人进行调查分析，并将抽取的学生的数学解题成绩进行分组，绘制如下频数分布表和成绩分布扇形统计图（图1）：
该校90名学生数学解题成绩频数分布表
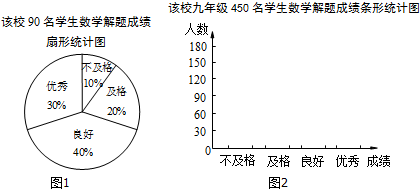
（1）根据抽样调查的结果，将估计出该校九年级450名学生数学解题成绩情况在图2中绘制成条形统计图：
（2）请你结合上述统计的结果，提出一条合理化建议．
该校90名学生数学解题成绩频数分布表
| 成绩 | 划记 | 频数 |
| 不及格 | 正 | 9 |
| 及格 | 正正正 | 18 |
| 良好 | 正正正正正正一 | 36 |
| 优秀 | 正正正正正 | 27 |
| 合计 | 90 |
（1）根据抽样调查的结果，将估计出该校九年级450名学生数学解题成绩情况在图2中绘制成条形统计图：
（2）请你结合上述统计的结果，提出一条合理化建议．
16．由4名同学每人写一个实系数一元二次方程，所得的四个方程中恰有两个无实数根的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{5}$ | D． | $\frac{3}{8}$ |
如图，直线AB∥CD，BC平分∠ABD，∠1=65°，求∠2的度数50°．