观察图形中点的个数.若按其规律再画下去.可以得到第105个图形中所有点的个数为( )A．1016个B．11025个C．11236个D．22249个题目和参考答案——青夏教育精英家教网——

题目内容

16．观察图形中点的个数，若按其规律再画下去，可以得到第105个图形中所有点的个数为（　　）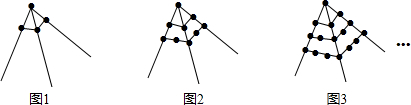

A．

1016个

B．

11025个

C．

11236个

D．

22249个

分析观察不难发现，点的个数依次为连续奇数的和，写出第n个图形中点的个数的表达式，再根据求和公式列式计算即可得解．

解答解：第1个图形中点的个数为：1+3=4，
第2个图形中点的个数为：1+3+5=9，
第3个图形中点的个数为：1+3+5+7=16，
…，
第n个图形中点的个数为：1+3+5+…+（2n+1）=$\frac{（1+2n+1）（n+1）}{2}$=（n+1）²．
当n=105时，（105+1）²=11236，
故选C．

点评本题是对图形变化规律的考查，比较简单，观察出点的个数是连续奇数的和是解题的关键，还要注意求和公式的利用．

练习册系列答案

优化学案系列答案

体验型学案系列答案

周周大考卷系列答案

激活思维优加课堂系列答案

全能达标100分系列答案

智能考核卷系列答案

活力试卷系列答案

琢玉计划系列答案

小学全能测试卷系列答案

名校全优考卷系列答案

相关题目

阅读：|5-2|表示5与2差的绝对值，也可理解为5与2两位数在数轴上所对应的两点之间的距离；|5+2|可以看做|5-（-2）|，表示5与-2的差的绝对值，也可理解为5与-2两位数在数轴上所对应的两点之间的距离，探索：
（1）如图，点A，B在数轴上对应的实数分别为m，n，则A，B间的距离是（用含m，n的式子表示）n-m；
（2）利用数轴，找出所有符合条件的整数x，使x所表示的点到5和-2的距离之和为7；
（3）由以上探索猜想对于任何有理数x，|x+3|+|x-6|是否有最小值？如果有，直接写出最小值；如果没有，说明理由．

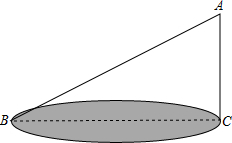公园有三个景点A、B、C构成如图所示的直角三角形，由于B、C两景点之间有一山相隔，为方便游客，准备在B、C间挖条隧道．已知∠ACB=90°，AB=3千米，AC=2千米．试用计算器探索：这条隧道至少要修多少米？（精确到1米）

如图，将一根30cm长的细木棒放入长、宽、高分别为8cm、6cm、24cm的长方体无盖盒子中，那么细木棒露在盒外面的最短长度是多少？

11．如图，边长为1的等边三角形ABC从图示的位置开始在数轴上顺时针无滑动地向右滚动，当三角形的一个顶点落在x=2015处时．三角形停止滚动．
①落在x=2015处的点是△ABC的哪个顶点？说明理由．
②在滚动过程中，点A走过的路程是多少？

1．用多项式填空，并指出它们的项和次数．
（1）温度由32°下降t℃是32-t℃，项为32，-t，次数为1次．
（2）甲数x²的$\frac{1}{2}$与乙数y²的和是$\frac{1}{2}$x²+y²，项为$\frac{1}{2}$x²，y²，次数为二次．

如图，有一张边长为6的正方形纸片ABCD，P是AD边上一点（不与点A、D重合），将正方形纸片沿EF折叠，使点B落在点P处，点C落在点G处，PG交DC于H，连接BP．
（1）求证：∠APB=∠BPH；
（2）若P为AD中点，求四边形EFGP的面积；
（3）当点P在边AD上移动时，△PDH的周长是否发生变化？写出你的结论并证明．

5．分解因式：2a²-b²-ab+2bc+4ac．

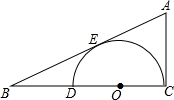如图，在Rt△ABC中，∠C=Rt∠．D为BC边上一点，以CD为直径作圆O，与AB相切于点E．若CD=2，BD=1.2，求点A到⊙O的切线长．