题目内容
8. 如图,有一张边长为6的正方形纸片ABCD,P是AD边上一点(不与点A、D重合),将正方形纸片沿EF折叠,使点B落在点P处,点C落在点G处,PG交DC于H,连接BP.
如图,有一张边长为6的正方形纸片ABCD,P是AD边上一点(不与点A、D重合),将正方形纸片沿EF折叠,使点B落在点P处,点C落在点G处,PG交DC于H,连接BP.(1)求证:∠APB=∠BPH;
(2)若P为AD中点,求四边形EFGP的面积;
(3)当点P在边AD上移动时,△PDH的周长是否发生变化?写出你的结论并证明.
分析 (1)欲证明∠APB=∠BPH,只要证明∠APB+∠EBP=90°,∠BPH+∠EPB=90°,根据EP=EB,推出∠EBP=∠EPB即可证明.
(2)如图1中,作FM⊥AB于M.由△ABP≌△MFE,推出AP=EM=3,想办法求出EB、CF即可解决问题.
(3)△PHD的周长不变为定值12.如图2中,作BQ⊥PG于Q,连接BH,分别证明△BPA≌△BPQ和△BHQ≌△BHC即可.
解答 (1)证明:∵PE=BE,
∴∠EBP=∠EPB,
∵∠A=∠ABC=∠EPG=90°,
∴∠APB+∠EBP=90°,∠BPH+∠EPB=90°,
∴∠APB=∠BPH.
(2)解:如图1中,作FM⊥AB于M.
∵∠BEF+∠ABP=90°,∠BEF+∠EFM=90°,
∴∠ABP=∠EFM,
在△ABP和△MFE中,
$\left\{\begin{array}{l}{∠A∠FME}\\{AB=MF}\\{∠ABP=∠EFM}\end{array}\right.$,
∴△ABP≌△MFE,
∴ME=AP=$\frac{1}{2}$AD=3,
在Rt△AEP中,设AE=x,则EP=BE=6-x,
∴(6-x)2=x2+32,
∴x=$\frac{9}{4}$,
∴CF=BM-AB-AE-EM=$\frac{3}{4}$,
∴S四边形EFGP=$\frac{1}{2}$×(CF+BE)×BC=$\frac{1}{2}$×($\frac{3}{4}$+$\frac{15}{4}$)×6=$\frac{27}{2}$.
(3)解:△PHD的周长不变为定值12.
证明:如图2中,作BQ⊥PG于Q,连接BH.
由(1)可知∠APB=∠BPQ,
在△BPA和△BPQ中,
$\left\{\begin{array}{l}{∠A=∠BQP=90°}\\{∠APB=∠BPQ}\\{BP=BP}\end{array}\right.$,
∴△BPA≌△BPQ,
∴AP=PQ,AB=BQ,
∵AB=BC,
∴BC=BQ,
∵∠BQH=∠C=90°,BH=BH,
∴△BHQ≌△BHC,
∴CH=QH,
∴△PDH的周长=DP+PH+DH=(DP+AP)+(CH+DH)=AD+CD=12.
点评 本题考查四边形综合题、翻折变换、正方形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.

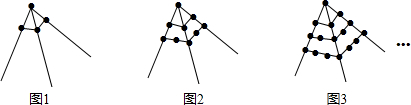
| A. | 1016个 | B. | 11025个 | C. | 11236个 | D. | 22249个 |
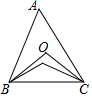 在如图所示的锐角三角形ABC中,O是其外接圆圆心,I是其内切圆圆心,若∠BOC=∠BIC,则sinA的值是( )
在如图所示的锐角三角形ABC中,O是其外接圆圆心,I是其内切圆圆心,若∠BOC=∠BIC,则sinA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
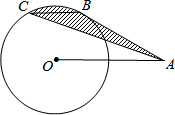 如图所示,A是半径为1的⊙O外的一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥OA,连接AC,则阴影部分的面积等于( )
如图所示,A是半径为1的⊙O外的一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥OA,连接AC,则阴影部分的面积等于( )| A. | $\frac{2π}{9}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{6}+\frac{\sqrt{3}}{8}$ | D. | $\frac{π}{4}-\frac{\sqrt{3}}{8}$ |
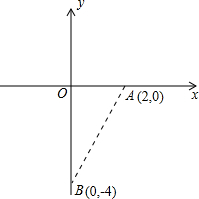 在直角坐标系中,以点A(2,0)为圆心作圆,使圆经过点B(0,-4),如图所示,试判断C(0,4)、D(-2,0)、E(0,8)与⊙A的位置关系.若点M(0,m)在⊙A外,求m的取值范围.
在直角坐标系中,以点A(2,0)为圆心作圆,使圆经过点B(0,-4),如图所示,试判断C(0,4)、D(-2,0)、E(0,8)与⊙A的位置关系.若点M(0,m)在⊙A外,求m的取值范围.