题目内容
6.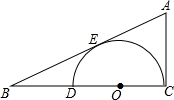 如图,在Rt△ABC中,∠C=Rt∠.D为BC边上一点,以CD为直径作圆O,与AB相切于点E.若CD=2,BD=1.2,求点A到⊙O的切线长.
如图,在Rt△ABC中,∠C=Rt∠.D为BC边上一点,以CD为直径作圆O,与AB相切于点E.若CD=2,BD=1.2,求点A到⊙O的切线长.
分析 连接OE,在Rt△BOE中可求得BE,由条件可知AC是⊙O的切线,可知AE=AC,设AC=AE=x,在Rt△ABC中由勾股定理可列方程,可求得AC的长.
解答 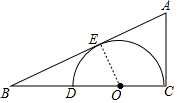 解:
解:
连接OE,
∵AB是⊙O的切线,
∴OE⊥AB,
∵CD=2,
∴OD=OE=1,
∴BO=BD+OD=1.2+1=2.2,
在Rt△BOE中,由勾股定理可得BE=$\sqrt{B{O}^{2}-O{E}^{2}}$=$\sqrt{2.{2}^{2}-1}$=$\frac{4\sqrt{6}}{5}$,
∵∠C=90°,且CD为直径,
∴AC是⊙O的切线,
∴AE=AC,
设AE=AC=x,则AB=$\frac{4\sqrt{6}}{5}$+x,
在Rt△ABC中,由勾股定理可得AB2=BC2+AC2,
∴(x+$\frac{4\sqrt{6}}{5}$)2=3.22+x2,解得x=$\frac{2\sqrt{6}}{3}$,
即点A到⊙O的切线长为$\frac{2\sqrt{6}}{3}$.
点评 本题主要考查切线的性质和判定,掌握过切点的半径与切线垂直是解题的关键.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
16.观察图形中点的个数,若按其规律再画下去,可以得到第105个图形中所有点的个数 为( )
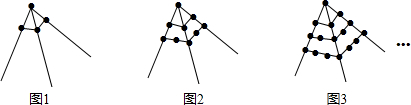

| A. | 1016个 | B. | 11025个 | C. | 11236个 | D. | 22249个 |
17.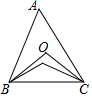 在如图所示的锐角三角形ABC中,O是其外接圆圆心,I是其内切圆圆心,若∠BOC=∠BIC,则sinA的值是( )
在如图所示的锐角三角形ABC中,O是其外接圆圆心,I是其内切圆圆心,若∠BOC=∠BIC,则sinA的值是( )
 在如图所示的锐角三角形ABC中,O是其外接圆圆心,I是其内切圆圆心,若∠BOC=∠BIC,则sinA的值是( )
在如图所示的锐角三角形ABC中,O是其外接圆圆心,I是其内切圆圆心,若∠BOC=∠BIC,则sinA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
18.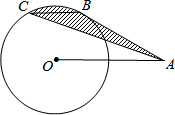 如图所示,A是半径为1的⊙O外的一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥OA,连接AC,则阴影部分的面积等于( )
如图所示,A是半径为1的⊙O外的一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥OA,连接AC,则阴影部分的面积等于( )
 如图所示,A是半径为1的⊙O外的一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥OA,连接AC,则阴影部分的面积等于( )
如图所示,A是半径为1的⊙O外的一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥OA,连接AC,则阴影部分的面积等于( )| A. | $\frac{2π}{9}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{6}+\frac{\sqrt{3}}{8}$ | D. | $\frac{π}{4}-\frac{\sqrt{3}}{8}$ |
15.《中国县域经济发展报告(2016)》于2016年9月22日在京发布,启东跻身“全国县域经济综合竞争力100强”,位列第22名,比去年上升了5位;今年前三季度,启东全市实现地区生产总值717亿元,717亿用科学记数法表示为( )
| A. | 7.17×109 | B. | 7.17×1010 | C. | 7.17×1011 | D. | 7.17×1012 |
 如图,已知点E是正方形ABCD的边BC上的一点,把线段AE绕点E顺时针旋转90°得到线段EF,连接CF,AF.
如图,已知点E是正方形ABCD的边BC上的一点,把线段AE绕点E顺时针旋转90°得到线段EF,连接CF,AF.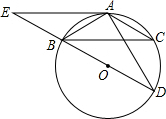 如图,△ABC为⊙O的内接三角形,BD为⊙O的直径,∠ABC=∠D,AC=2$\sqrt{3}$,AD=6,延长DB到E,使BE=BO,连接EA,那么直线EA与⊙O相切吗?为什么?
如图,△ABC为⊙O的内接三角形,BD为⊙O的直径,∠ABC=∠D,AC=2$\sqrt{3}$,AD=6,延长DB到E,使BE=BO,连接EA,那么直线EA与⊙O相切吗?为什么?