题目内容
4．已知（a-2）x2-2ax+a+1=0没有实数根，求a的取值范围．分析 当a=0，方程为一元一次方程，当a≠0时，利用根的判别式△＜0，求出a的取值范围即可．
解答 解：当a=2时，方程为-4x+3=0，方程有实数根，
当a≠2时，
∵（a-2）x2-2ax+a+1=0没有实数根，
∴△＜0，
∴（-2a）2-4（a-2）（a+1）＜0，
∴a＜2．
综上a的取值范围为a＜2．
点评 本题考查了根的判别式以及一元二次方程的定义，解答本题的关键是掌握一元二次方程根的情况与判别式△的关系：△＜0?方程没有实数根．
练习册系列答案
相关题目
14．Rt△ABC中，∠C=90°，AC=3，BC=4，把它沿AC所在直线旋转一周，则所得几何体的侧面积是（ ）
| A． | 12π | B． | 15π | C． | 20π | D． | 36π |
15．
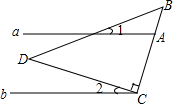如图，直线a∥b，直角三角形如图放置，∠DCB=90°．若∠2+∠B=70°，则∠1的度数为（ ）
如图，直线a∥b，直角三角形如图放置，∠DCB=90°．若∠2+∠B=70°，则∠1的度数为（ ）| A． | 40° | B． | 30° | C． | 25° | D． | 20° |
13．
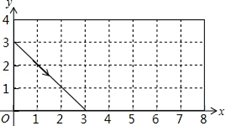如图，动点P从（0，3）出发，沿所示方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点P第2015次碰到矩形的边时，点P的坐标为（ ）
如图，动点P从（0，3）出发，沿所示方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点P第2015次碰到矩形的边时，点P的坐标为（ ）| A． | （3，0） | B． | （7，4） | C． | （8，1） | D． | （1，4） |
14．计算多项式-2x（3x-2）2+3除以3x-2后，所得商式与余式两者之和为何？（ ）
| A． | -2x+3 | B． | -6x2+4x | C． | -6x2+4x+3 | D． | -6x2-4x+3 |