题目内容
14.Rt△ABC中,∠C=90°,AC=3,BC=4,把它沿AC所在直线旋转一周,则所得几何体的侧面积是( )| A. | 12π | B. | 15π | C. | 20π | D. | 36π |
分析 先利用勾股定理计算出AB=5,然后根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解.
解答  解:Rt△ABC沿AC所在直线旋转一周,所得几何体为圆锥,母线AB的长=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
解:Rt△ABC沿AC所在直线旋转一周,所得几何体为圆锥,母线AB的长=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
所以圆锥的侧面积=$\frac{1}{2}$•2π•4•5=20π.
故选C.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
4.下列说法正确的是( )
| A. | “打开电视机,正在播足球赛”是必然事件 | |
| B. | 一组数据2,4,5,5,3,6的众数和中位数都是5 | |
| C. | 甲乙两组数据的方差分别是S甲2=0.14,S乙2=0.09,则乙组数据比甲组数据稳定 | |
| D. | “掷一枚硬币正面朝上的概率是$\frac{1}{2}$”表示每抛硬币2次就有1次正面上 |
5.某商场购进商品后加价40%作为销售价,商场搞优惠促销活动,决定甲、乙商品分别以七折和九折销售,某顾客购买甲、乙两种商品,共付款399元,这两种商品售价之和为490元,问这两种商品进价分别为多少元.
2.下列命题中,假命题是( )
| A. | 半圆(或直径)所对的圆周角是直角 | B. | 对顶角相等 | ||
| C. | 四条边相等的四边形是菱形 | D. | 对角线相等的四边形是平行四边形 |
6.-$\frac{1}{7}$的倒数是( )
| A. | -7 | B. | 7 | C. | $\frac{1}{7}$ | D. | -$\frac{1}{7}$ |
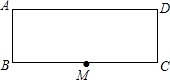 如图,在矩形ABCD中,AB=5,BC=24,M是BC的中点,若点P为线段AD上的一点,连接AM、PM,△PAM是以AP为腰的等腰三角形,则AP的长为13或$\frac{169}{24}$.
如图,在矩形ABCD中,AB=5,BC=24,M是BC的中点,若点P为线段AD上的一点,连接AM、PM,△PAM是以AP为腰的等腰三角形,则AP的长为13或$\frac{169}{24}$.