题目内容
12.下列函数:①y=-x;②y=-$\frac{1}{x}$;③y=2x+1;④y=x2(x<0),y随x的增大而减小的函数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 本题综合运用了一次函数,反比例函数,二次函数的增减性,需要根据这些函数的性质及自变量的取值范围,逐一判断.
解答 解:根据函数的性质可知,y随x的增大而减小的函数有:①y=-x;④y=x2(x<0).
故选B.
点评 本题考查了二次函数、一次函数、反比例函数的增减性(单调性),是一道难度中等的题目.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
2.下列命题中,假命题是( )
| A. | 半圆(或直径)所对的圆周角是直角 | B. | 对顶角相等 | ||
| C. | 四条边相等的四边形是菱形 | D. | 对角线相等的四边形是平行四边形 |
7.函数y=-x2+2x+2的顶点坐标是( )
| A. | (1,3) | B. | (-1,3) | C. | (1,-2) | D. | (-1,2) |
1.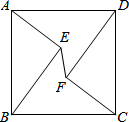 如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为( )
如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为( )
 如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为( )
如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}\sqrt{2}$ | C. | $\frac{7}{5}$ | D. | $\sqrt{2}$ |
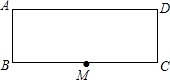 如图,在矩形ABCD中,AB=5,BC=24,M是BC的中点,若点P为线段AD上的一点,连接AM、PM,△PAM是以AP为腰的等腰三角形,则AP的长为13或$\frac{169}{24}$.
如图,在矩形ABCD中,AB=5,BC=24,M是BC的中点,若点P为线段AD上的一点,连接AM、PM,△PAM是以AP为腰的等腰三角形,则AP的长为13或$\frac{169}{24}$. 如图,已知∠AOB=60°,点P在边OA上,OP=8,点M,N在边OB上,PM=PN,若MN=2,则ON=( )
如图,已知∠AOB=60°,点P在边OA上,OP=8,点M,N在边OB上,PM=PN,若MN=2,则ON=( )