题目内容
20.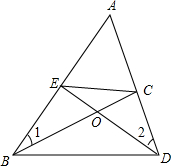 如图,△ABD中,点E、C分别在AB、AD上,BC与DE相交于点O,若∠1=∠2.求证:
如图,△ABD中,点E、C分别在AB、AD上,BC与DE相交于点O,若∠1=∠2.求证:(1)△BOD∽△EOC;
(2)△ACE∽△ABD.
分析 (1)根据有两组角对应相等的两个三角形相似,由∠1=∠2,∠BOE=∠DOC可判断△BOE∽△DOC,则$\frac{BO}{DO}$=$\frac{EO}{CO}$,利用比例性质得$\frac{BO}{EO}$=$\frac{DO}{CO}$,加上∠BOD=∠COE,则根据两组对应边的比相等且夹角对应相等的两个三角形相似可判断△BOD∽△EOC;
(2)与(1)证明方法一样:由∠1=∠2,∠BAC=∠DAE可证明△ABC∽△ADE,则$\frac{AB}{AD}$=$\frac{AC}{AE}$,利用比例性质得$\frac{AB}{AC}$=$\frac{AD}{AE}$,加上∠CAE=∠BAD,则可判断△ACE∽△ABD.
解答 (1)证明:∵∠1=∠2,∠BOE=∠DOC,
∴△BOE∽△DOC,
∴$\frac{BO}{DO}$=$\frac{EO}{CO}$,
∴$\frac{BO}{EO}$=$\frac{DO}{CO}$,
而∠BOD=∠COE,
∴△BOD∽△EOC;
(2)证明:∵∠1=∠2,∠BAC=∠DAE,
∴△ABC∽△ADE,
∴$\frac{AB}{AD}$=$\frac{AC}{AE}$,
∴$\frac{AB}{AC}$=$\frac{AD}{AE}$,
而∠CAE=∠BAD,
∴△ACE∽△ABD.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.也考查了相似三角形的性质.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
12.写出满足如表条件的一次函数表达式为y=-3x+1.
| x | -1 | 0 | 1 | 2 |
| y | 4 | 1 | -2 | -5 |
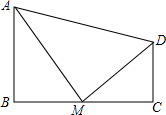 如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证:
如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证: 如图,P是△ABC内一点,延长BP交AC于点D,若∠3=25°,∠A=67°,∠4=40°,则∠1的度数是多少?
如图,P是△ABC内一点,延长BP交AC于点D,若∠3=25°,∠A=67°,∠4=40°,则∠1的度数是多少? 如图,点A、B、C在⊙O上,点D在⊙O内,比较∠BAC与∠BDC的大小.
如图,点A、B、C在⊙O上,点D在⊙O内,比较∠BAC与∠BDC的大小. 如图,已知AC与BD相交于点O,AD∥BC,且AO=OD.求证:OB=OC.
如图,已知AC与BD相交于点O,AD∥BC,且AO=OD.求证:OB=OC. 如图,△ABC中,D、E分别是AB,AC边上的中点,连接DE并延长使EF=DE,连接DC、CF、AF
如图,△ABC中,D、E分别是AB,AC边上的中点,连接DE并延长使EF=DE,连接DC、CF、AF