题目内容
10.A是⊙O外一点,直线AO交⊙O于C,D两点,E是⊙O上的一点(不与C,D重合),连接AE交⊙O于点B,AB=OC.(1)当点B在线段AE上时,如图1所示,求∠DOE与∠A之间的关系;
(2)当点E在线段AB上时,如图2所示,则(1)中的结论还成立吗?说明理由.
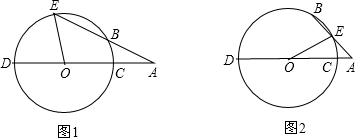
分析 (1)连接OB,则OB=OC,根据等边对等角得出∠1=∠A,∠2=∠E,进而根据三角形外角的性质求得∠E=2∠A,得出∠DOE=∠E+∠A=3∠A;
(2)连接OB,则OB=OC,根据等边对等角得出∠AOB=∠A,∠OBE=∠OEB,进而根据三角形内角和定理求得即可求得∴∠DOE=∠BOD+∠BOE=180°-∠AOB+∠BOE=180°-∠A+4∠A-180°=3∠A.
解答 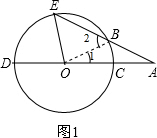 解:(1)∠DOE=3∠A;
解:(1)∠DOE=3∠A;
连接OB,则OB=OC,
∵AB=OC.
∴OB=AB,
∴∠1=∠A,
∵OE=OB,
∴∠2=∠E,
∵∠2=∠1+∠A=2∠A,
∴∠E=2∠A,
∴∠DOE=∠E+∠A=3∠A;
(2)成立;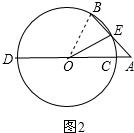
连接OB,则OB=OC,
∵AB=OC.
∴OB=AB,
∴∠AOB=∠A,
∴∠B=180°-2∠A,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠BOE=180°-2∠B=180°-2(180°-2∠A)=4∠A-180°,
∴∠DOE=∠BOD+∠BOE=180°-∠AOB+∠BOE=180°-∠A+4∠A-180°=3∠A.
点评 本题考查了等腰三角形的性质,三角形外角的性质以及三角形内角和定理,熟练掌握性质定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.在下列多项式乘法中,不能用平方差公式计算的是( )
| A. | (a-b)(-a+b) | B. | (m3-n3)(m3+n3) | C. | (-7-x)(7-x) | D. | (x2-y2)(y2+x2) |
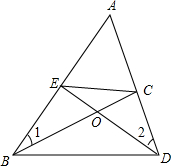 如图,△ABD中,点E、C分别在AB、AD上,BC与DE相交于点O,若∠1=∠2.求证:
如图,△ABD中,点E、C分别在AB、AD上,BC与DE相交于点O,若∠1=∠2.求证:



 如图,E是四边形ADBC内的一点,连接AE,CE,DE,AB,如果$\frac{DE}{BC}$=$\frac{AE}{AC}$=$\frac{AD}{AB}$,△ADB与△AEC相似吗?为什么?
如图,E是四边形ADBC内的一点,连接AE,CE,DE,AB,如果$\frac{DE}{BC}$=$\frac{AE}{AC}$=$\frac{AD}{AB}$,△ADB与△AEC相似吗?为什么? 如图,在△ABC中,∠A=90°,E为BC上一点,A和E关于BD对称,B点和C点关于DE对称,则∠C的度数为30°.
如图,在△ABC中,∠A=90°,E为BC上一点,A和E关于BD对称,B点和C点关于DE对称,则∠C的度数为30°. 一个正方体木块的六个面上分别写着数字1,2,3,4,5,6,滚动后的图如图所示,则写4的这个面的对面写有3.
一个正方体木块的六个面上分别写着数字1,2,3,4,5,6,滚动后的图如图所示,则写4的这个面的对面写有3.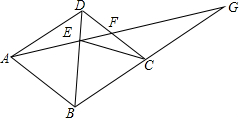 已知四边形ABCD是菱形,G是BC延长线上一点,AG交BD于点E,交CD于点K,若EF=4,FG=5,求CE的长.
已知四边形ABCD是菱形,G是BC延长线上一点,AG交BD于点E,交CD于点K,若EF=4,FG=5,求CE的长.