题目内容
5. 如图,△ABC中,D、E分别是AB,AC边上的中点,连接DE并延长使EF=DE,连接DC、CF、AF
如图,△ABC中,D、E分别是AB,AC边上的中点,连接DE并延长使EF=DE,连接DC、CF、AF(1)四边形ADCF时怎样的四边形?证明你的结论;
(2)当△ABC满足什么条件时,四边形ADCF是矩形?
分析 (1)根据“对角线互相平分的四边形为平行四边形”推知四边形ADCF是平行四边形.
(2)由“对角线相等的平行四边形是矩形”可以推导:AC=BC.
解答 解: (1)∵点E是边AC的中点,
(1)∵点E是边AC的中点,
∴AE=CE.
又∵EF=DE,
∴四边形ADCF是平行四边形.
(2)当AC=BC时,平行四边形ADCF是矩形.
理由:∵四边形ADCF是矩形,
∴AC=DF.
∵在△ABC中,D、E分别是AB,AC边上的中点,
∴DE是△ABC的中位线,
∴DE=$\frac{1}{2}$BC.
又∵EF=DE,
∴DF=BC,
∴AC=BC.
点评 本题考查了平行四边形的判定与性质以及矩形的判定与性质.证明一个四边形是矩形,若题设条件与这个四边形的对角线有关,通常证这个四边形的对角线相等.

练习册系列答案
相关题目
15.已知一个等腰三角形两内角的度数之比为1:2,则这个等腰三角形顶角的度数为( )
| A. | 36° | B. | 36°或90° | C. | 90° | D. | 60° |
17.下列根式是最简二次根式的是( )
| A. | $\sqrt{0.3}$ | B. | $\sqrt{{a}^{2}-{b}^{2}}$ | C. | $\sqrt{{a}^{2}b}$ | D. | $\sqrt{12}$ |
15.在下列多项式乘法中,不能用平方差公式计算的是( )
| A. | (a-b)(-a+b) | B. | (m3-n3)(m3+n3) | C. | (-7-x)(7-x) | D. | (x2-y2)(y2+x2) |
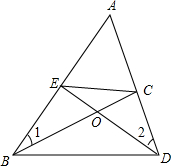 如图,△ABD中,点E、C分别在AB、AD上,BC与DE相交于点O,若∠1=∠2.求证:
如图,△ABD中,点E、C分别在AB、AD上,BC与DE相交于点O,若∠1=∠2.求证: