题目内容
10.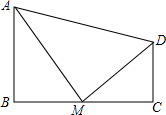 如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证:
如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证:(1)AM⊥DM;
(2)M为BC的中点.
分析 (1)根据平行线的性质得到∠BAD+∠ADC=180°,根据角平分线的定义得到∠MAD+∠ADM=90°,根据垂直的定义得到答案;
(2)作NM⊥AD,根据角平分线的性质得到BM=MN,MN=CM,等量代换得到答案.
解答 解:(1)∵AB∥CD,
∴∠BAD+∠ADC=180°,
∵AM平分∠BAD,DM平分∠ADC,
∴2∠MAD+2∠ADM=180°,
∴∠MAD+∠ADM=90°,
∴∠AMD=90°,
即AM⊥DM;
(2)作NM⊥AD交AD于N,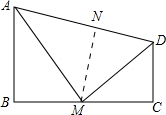
∵∠B=90°,AB∥CD,
∴BM⊥AB,CM⊥CD,
∵AM平分∠BAD,DM平分∠ADC,
∴BM=MN,MN=CM,
∴BM=CM,
即M为BC的中点.
点评 本题考查的是角平分线的性质,掌握平行线的性质和角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
15.已知一个等腰三角形两内角的度数之比为1:2,则这个等腰三角形顶角的度数为( )
| A. | 36° | B. | 36°或90° | C. | 90° | D. | 60° |
19.填写表
| 方程 | 一般形式 | 二次项系数 | 一次项系数 | 常数项 |
| (1)x2-x=2 | x2-x-2=0 | 1 | -1 | -2 |
| (2)4x+1=x2 | x2-4x-1=0 | 1 | -4 | -1 |
| (3)x(x+3)=-2 | x2+3x+2=0 | 1 | 3 | 2 |
| (4)(2x+1)(3x-2)=3 | 6x2-x-5=0 | 6 | -1 | -5 |
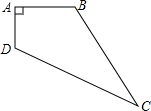 如图,一块四边形的土地,其中∠DAB=90°,AB=4m,AD=3m,BC=12m,CD=13m,则这块土地的面积是36m2.
如图,一块四边形的土地,其中∠DAB=90°,AB=4m,AD=3m,BC=12m,CD=13m,则这块土地的面积是36m2.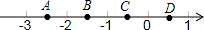 如图数轴上有A、B、C、D四点,根据图中各点的位置,判断那一点所表示的数与$\frac{\sqrt{2}}{2}$最接近的是( )
如图数轴上有A、B、C、D四点,根据图中各点的位置,判断那一点所表示的数与$\frac{\sqrt{2}}{2}$最接近的是( )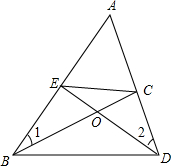 如图,△ABD中,点E、C分别在AB、AD上,BC与DE相交于点O,若∠1=∠2.求证:
如图,△ABD中,点E、C分别在AB、AD上,BC与DE相交于点O,若∠1=∠2.求证: