题目内容
 抛物线y=ax2+bx+c(a≠0)向右平移2个单位得到抛物线y=a(x-3)2-1,且平移后的抛物线经过点A(2,1).
抛物线y=ax2+bx+c(a≠0)向右平移2个单位得到抛物线y=a(x-3)2-1,且平移后的抛物线经过点A(2,1).(1)求平移后抛物线的解析式;
(2)设原抛物线与y轴的交点为B,顶点为P,平移后抛物线的对称轴与x轴交于点M,求△BPM的面积.
考点:二次函数图象与几何变换
专题:
分析:(1)把点A代入平移后的抛物线y=a(x-3)2-1来求a的值;
(2)根据平移前、后的函数解析式,然后求出B、P、M三点的坐标,根据三角形的面积公式即可求出△BPM的面积.
(2)根据平移前、后的函数解析式,然后求出B、P、M三点的坐标,根据三角形的面积公式即可求出△BPM的面积.
解答: 解:(1)把点A(2,1)代入y=a(x-3)2-1,得
解:(1)把点A(2,1)代入y=a(x-3)2-1,得
1=a(2-3)2-1,
整理,得
1=a-1,
解得 a=2.
则平移后的抛物线解析式为:y=2(x-3)2-1;
(2)由(1)知,平移后的抛物线解析式为:y=2(x-3)2-1,则M(3,0)
∵抛物线y=ax2+bx+c(a≠0)向右平移2个单位得到抛物线y=2(x-3)2-1,
∴平移前的抛物线解析式为:y=2(x-1)2-1.
∴P(1,-1).
令x=0,则y=1.
故B(0,1),
∴BM=
易推知BM2=BP2+PM2,即△BPM为直角三角形,
∴S△BPM=
BP•MP=
×
×
=
.
 解:(1)把点A(2,1)代入y=a(x-3)2-1,得
解:(1)把点A(2,1)代入y=a(x-3)2-1,得1=a(2-3)2-1,
整理,得
1=a-1,
解得 a=2.
则平移后的抛物线解析式为:y=2(x-3)2-1;
(2)由(1)知,平移后的抛物线解析式为:y=2(x-3)2-1,则M(3,0)
∵抛物线y=ax2+bx+c(a≠0)向右平移2个单位得到抛物线y=2(x-3)2-1,
∴平移前的抛物线解析式为:y=2(x-1)2-1.
∴P(1,-1).
令x=0,则y=1.
故B(0,1),
∴BM=
| 10 |
易推知BM2=BP2+PM2,即△BPM为直角三角形,
∴S△BPM=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |
| 2 |
点评:本题主要考查了二次函数解析式的确定、图形的面积求法、函数图象交点等知识及综合应用知识、解决问题的能力.

练习册系列答案
相关题目
如果点G是△ABC的重心,联结AG并延长,交对边BC于点D,那么AG:AD是( )
| A、2:3 | B、1:2 |
| C、1:3 | D、3:4 |
抛物线y=-
x2的图象向右平移2个单位长度后所得新的抛物线的顶点坐标为( )
| 1 |
| 2 |
| A、(0,-2) |
| B、(0,2) |
| C、(-2,0) |
| D、(2,0) |
 据报道:2013年底我国微信用户规模已到达6亿.以下是根据相关数据制作的统计图表的一部分:
据报道:2013年底我国微信用户规模已到达6亿.以下是根据相关数据制作的统计图表的一部分:2012年及2013年电话、电信、微信的人均使用时长统计表 单位:分钟
| 分式 年份 |  电话 电话 |  短信 短信 |  微信 微信 |
| 2012年 | 14.4 | 4.1 | 3.0 |
| 2013年 | 5.1 | 3.4 | 9.7 |
①从2012年到2013年微信的人均使用时长增加了________分钟;②在我国6亿微信用户中,经常使用户约为_________亿(结果精确到0.1);③从调查数学看,预计我国微信用户今后每年将以20%的增长率递增,请你估计两年后,我国微信用户的规模将到达_________亿.( )
| A、6.7 2 8.5 |
| B、9 1.8 8.64 |
| C、6.7 1.5 8.64 |
| D、6 1.8 8.5 |
下列事件中,是确定事件的是( )
| A、1小时等于60分钟 |
| B、明天是晴天 |
| C、打雷后会下雨 |
| D、下雨后有彩虹 |
下列判断错误的是( )
A、0•
| ||||||||||||
B、如果
| ||||||||||||
C、设
| ||||||||||||
D、如果|
|
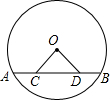 如图,AB是⊙O的弦,点C、D在弦AB上,且AD=BC,联结OC、OD.求证:△OCD是等腰三角形.
如图,AB是⊙O的弦,点C、D在弦AB上,且AD=BC,联结OC、OD.求证:△OCD是等腰三角形. 如图,三角板ABC中,∠ACB=90°,∠B=30°,AC=2
如图,三角板ABC中,∠ACB=90°,∠B=30°,AC=2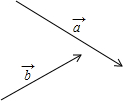 如图,已知两个不平行的向量
如图,已知两个不平行的向量