题目内容
在Rt△ABC中,已知∠C=90°,AC=3,BC=4,那么∠A的余弦值等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:锐角三角函数的定义
专题:
分析:先根据勾股定理,求出AB的值,然后由余弦=邻边÷斜边计算即可.
解答:解:在Rt△ABC中,∵∠C=90°,AC=3,BC=4,
∴AB=
=5,
∴cosA=
=
.
故选A.
∴AB=
| AC2+BC2 |
∴cosA=
| AC |
| AB |
| 3 |
| 5 |
故选A.
点评:本题考查了锐角三角函数的定义和勾股定理,牢记定义和定理是解题的关键.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
如果点G是△ABC的重心,联结AG并延长,交对边BC于点D,那么AG:AD是( )
| A、2:3 | B、1:2 |
| C、1:3 | D、3:4 |
下列说法正确的有( )个
①非负整数包括0和正整数;②射线AO和射线OA是同一条射线;③两点之间线段最短;④0是单项式;
⑤过直线外一点有且只有一条直线与这条直线平行;⑥若(x-3)2+|y+1|=0,则x+y=4.
①非负整数包括0和正整数;②射线AO和射线OA是同一条射线;③两点之间线段最短;④0是单项式;
⑤过直线外一点有且只有一条直线与这条直线平行;⑥若(x-3)2+|y+1|=0,则x+y=4.
| A、4 | B、5 | C、6 | D、3 |
在同圆或等圆中,下列说法错误的是( )
| A、相等弦所对的弧相等 |
| B、相等弦所对的圆心角相等 |
| C、相等圆心角所对的弧相等 |
| D、相等圆心角所对的弦相等 |
抛物线y=-
x2的图象向右平移2个单位长度后所得新的抛物线的顶点坐标为( )
| 1 |
| 2 |
| A、(0,-2) |
| B、(0,2) |
| C、(-2,0) |
| D、(2,0) |
 如图,在△ABC中,D是BC边上一点,BD=m,CD=n,则
如图,在△ABC中,D是BC边上一点,BD=m,CD=n,则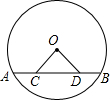 如图,AB是⊙O的弦,点C、D在弦AB上,且AD=BC,联结OC、OD.求证:△OCD是等腰三角形.
如图,AB是⊙O的弦,点C、D在弦AB上,且AD=BC,联结OC、OD.求证:△OCD是等腰三角形.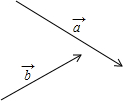 如图,已知两个不平行的向量
如图,已知两个不平行的向量