题目内容
已知直线y=3x+b经过点A(2,7),求不等式组3x+b≤0的解集.
考点:一次函数与一元一次不等式
专题:计算题
分析:先根据一次函数图象上点的坐标特征得到6+b=7,解得b=1,然后解不等式3x+1≤0即可.
解答:解:∵一次函数y=3x+b图象过点A(2,7),
∴6+b=7,解得b=1,
∴一次函数解析式为y=3x+1,
解不等式3x+1≤0得x≤-
,
即不等式kx+2≤0的解集为x≤-
.
∴6+b=7,解得b=1,
∴一次函数解析式为y=3x+1,
解不等式3x+1≤0得x≤-
| 1 |
| 3 |
即不等式kx+2≤0的解集为x≤-
| 1 |
| 3 |
点评:本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
如果点G是△ABC的重心,联结AG并延长,交对边BC于点D,那么AG:AD是( )
| A、2:3 | B、1:2 |
| C、1:3 | D、3:4 |
A、B、C三点分别表示家、学校、超市,若学校在家的南偏西78°方向,超市在家的北偏东24°方向,则∠BAC的度数为( )
| A、102° | B、126° |
| C、132° | D、123° |
下列说法正确的有( )个
①非负整数包括0和正整数;②射线AO和射线OA是同一条射线;③两点之间线段最短;④0是单项式;
⑤过直线外一点有且只有一条直线与这条直线平行;⑥若(x-3)2+|y+1|=0,则x+y=4.
①非负整数包括0和正整数;②射线AO和射线OA是同一条射线;③两点之间线段最短;④0是单项式;
⑤过直线外一点有且只有一条直线与这条直线平行;⑥若(x-3)2+|y+1|=0,则x+y=4.
| A、4 | B、5 | C、6 | D、3 |
下列事件中,是确定事件的是( )
| A、1小时等于60分钟 |
| B、明天是晴天 |
| C、打雷后会下雨 |
| D、下雨后有彩虹 |
 如图,OA的方向是北偏东15度,OB的方向是西偏北50度,若∠AOC=∠AOB,则OC的方向是
如图,OA的方向是北偏东15度,OB的方向是西偏北50度,若∠AOC=∠AOB,则OC的方向是 如图,在△ABC中,D是BC边上一点,BD=m,CD=n,则
如图,在△ABC中,D是BC边上一点,BD=m,CD=n,则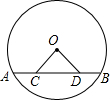 如图,AB是⊙O的弦,点C、D在弦AB上,且AD=BC,联结OC、OD.求证:△OCD是等腰三角形.
如图,AB是⊙O的弦,点C、D在弦AB上,且AD=BC,联结OC、OD.求证:△OCD是等腰三角形.