题目内容
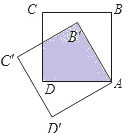 如图,正方形ABCD绕点A逆时针旋转,得到正方形AB′C′D′,当两正方形重叠部分的面积是原正方形面积的
如图,正方形ABCD绕点A逆时针旋转,得到正方形AB′C′D′,当两正方形重叠部分的面积是原正方形面积的| 1 |
| 4 |
| 1 |
| 2 |
考点:旋转的性质
专题:计算题
分析:B′C′交CD于E,如图,根据旋转的性质得AB′=AD,∠B′=∠D=90°,再证明Rt△ADE≌Rt△AB′E,得到S△ADE=S△AB′E,∠1=∠2,则S△ADE=
S正方形ABCD,即
AD•DE=
•AD•AD,所以DE=
AD,接着在Rt△ADE中利用勾股定理计算出AE=
DE,然后利用正弦的定义得sin∠2=
=
,即sin
∠B′AD=
.
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 4 |
| 17 |
| DE |
| AE |
| ||
| 17 |
| 1 |
| 2 |
| ||
| 17 |
解答: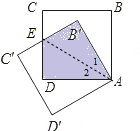 解:B′C′交CD于E,如图,
解:B′C′交CD于E,如图,
∵正方形ABCD绕点A逆时针旋转,得到正方形AB′C′D′,
∴AB′=AD,∠B′=∠D=90°,
在Rt△ADE和Rt△AB′E中,
,
∴Rt△ADE≌Rt△AB′E(HL),
∴S△ADE=S△AB′E,∠1=∠2,
∵两正方形重叠部分的面积是原正方形面积的
,
∴S△ADE=
S正方形ABCD,
∴
AD•DE=
•AD•AD,
∴DE=
AD,
在Rt△ADE中,AE=
=
=
DE,
∴sin∠2=
=
=
.
即sin
∠B′AD=
.
故答案为
.
 解:B′C′交CD于E,如图,
解:B′C′交CD于E,如图,∵正方形ABCD绕点A逆时针旋转,得到正方形AB′C′D′,
∴AB′=AD,∠B′=∠D=90°,
在Rt△ADE和Rt△AB′E中,
|
∴Rt△ADE≌Rt△AB′E(HL),
∴S△ADE=S△AB′E,∠1=∠2,
∵两正方形重叠部分的面积是原正方形面积的
| 1 |
| 4 |
∴S△ADE=
| 1 |
| 8 |
∴
| 1 |
| 2 |
| 1 |
| 8 |
∴DE=
| 1 |
| 4 |
在Rt△ADE中,AE=
| DE2+AD2 |
| DE2+16DE2 |
| 17 |
∴sin∠2=
| DE |
| AE |
| 1 | ||
|
| ||
| 17 |
即sin
| 1 |
| 2 |
| ||
| 17 |
故答案为
| ||
| 17 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质和锐角三角函数的定义.

练习册系列答案
相关题目
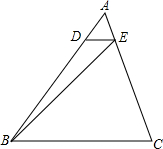 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,如果AE:EC=1:4,那么S△ADE:S△EBC=( )
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,如果AE:EC=1:4,那么S△ADE:S△EBC=( )| A、1:24 | B、1:20 |
| C、1:18 | D、1:16 |
如果点G是△ABC的重心,联结AG并延长,交对边BC于点D,那么AG:AD是( )
| A、2:3 | B、1:2 |
| C、1:3 | D、3:4 |
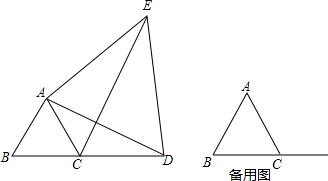

 如图,OA的方向是北偏东15度,OB的方向是西偏北50度,若∠AOC=∠AOB,则OC的方向是
如图,OA的方向是北偏东15度,OB的方向是西偏北50度,若∠AOC=∠AOB,则OC的方向是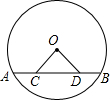 如图,AB是⊙O的弦,点C、D在弦AB上,且AD=BC,联结OC、OD.求证:△OCD是等腰三角形.
如图,AB是⊙O的弦,点C、D在弦AB上,且AD=BC,联结OC、OD.求证:△OCD是等腰三角形.