题目内容
12. 如图,点A,B,C都在格点上,请按要求回答问题或画图:
如图,点A,B,C都在格点上,请按要求回答问题或画图:(1)先将三角形ABC向右平移5格,再向上平移1格,可以得到三角形A1B1C1;
(2)先将三角形ABC向右平移2格,再向上平移5格,并记两次平移后得到的三角形为三角形A2B2C2,请画出这个三角形A2B2C2;
(3)连结AA2,BB2,CC2,图中一共有6组平行线段.
分析 (1)直接利用平移的性质得出平移规律;
(2)直接利用平移的性质得出△A2B2C2的位置;
(3)直接利用平移的性质得出平行线即可.
解答  解:(1)如图所示:△A1B1C1,即为所求;
解:(1)如图所示:△A1B1C1,即为所求;
故答案为:1;
(2)如图所示:△A2B2C2,即为所求;
(3)连结AA2,BB2,CC2,
AA2∥BB2,AA2∥CC2,BB2∥CC2,
AC∥A2C2,AB∥A2B2,BC∥B2C2,
图中一共有6组平行线段.
故答案为:6.
点评 此题主要考查了平移变换以及平移的性质,正确得出平移后对应点位置是解题关键.

练习册系列答案
相关题目
7.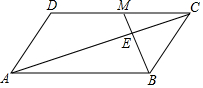 如图,在?ABCD中,∠ABC的平分线与对角线AC交于点E,与CD交于点M,已知BC=2,DM=3,?ABCD的面积为28,则△ABE的面积为( )
如图,在?ABCD中,∠ABC的平分线与对角线AC交于点E,与CD交于点M,已知BC=2,DM=3,?ABCD的面积为28,则△ABE的面积为( )
 如图,在?ABCD中,∠ABC的平分线与对角线AC交于点E,与CD交于点M,已知BC=2,DM=3,?ABCD的面积为28,则△ABE的面积为( )
如图,在?ABCD中,∠ABC的平分线与对角线AC交于点E,与CD交于点M,已知BC=2,DM=3,?ABCD的面积为28,则△ABE的面积为( )| A. | $\frac{28}{3}$ | B. | $\frac{21}{2}$ | C. | 10 | D. | $\frac{14}{3}$ |
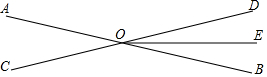 如图,直线AB,CD相交于点O,OE平分∠BOD;若∠AOD:∠BOE=8:1,求∠AOC的度数.
如图,直线AB,CD相交于点O,OE平分∠BOD;若∠AOD:∠BOE=8:1,求∠AOC的度数.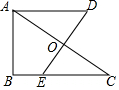 如图,Rt△ABC,∠B=90°,AC的垂直平分线交BC于点E,垂足为点O,过点A作BC的平行线,与直线OE交于点D,若AB=4,BC=6,则AD的长为$\frac{13}{3}$.
如图,Rt△ABC,∠B=90°,AC的垂直平分线交BC于点E,垂足为点O,过点A作BC的平行线,与直线OE交于点D,若AB=4,BC=6,则AD的长为$\frac{13}{3}$.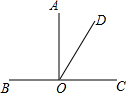 如图,AO⊥BC,垂足为O,且∠COD-∠AOD=34°28′.求∠BOD的度数.
如图,AO⊥BC,垂足为O,且∠COD-∠AOD=34°28′.求∠BOD的度数.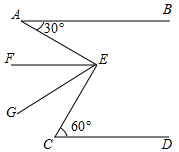 如图,AB∥CD,∠BAE=30°,∠ECD=60°,EF、EG等分∠AEC,试判断EF与AB的关系并写出你的理由.
如图,AB∥CD,∠BAE=30°,∠ECD=60°,EF、EG等分∠AEC,试判断EF与AB的关系并写出你的理由.