题目内容
2.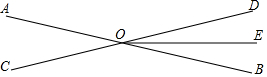 如图,直线AB,CD相交于点O,OE平分∠BOD;若∠AOD:∠BOE=8:1,求∠AOC的度数.
如图,直线AB,CD相交于点O,OE平分∠BOD;若∠AOD:∠BOE=8:1,求∠AOC的度数.
分析 先根据角平分线定义得出∠BOE=∠DOE,由∠AOD﹕∠BOE=8﹕1,得出∠AOD﹕∠BOE:∠DOE=8﹕1﹕1,再利用平角的定义得到∠AOD+∠DOE+BOE=180°,求出∠DOE=18°,最后根据对顶角相等即可求解.
解答 解:∵OE平分∠BOD,
∴∠BOE=∠DOE,
又∵∠AOD﹕∠BOE=8﹕1,
∴∠AOD﹕∠BOE:∠DOE=8﹕1﹕1,
又∵点A,O,B在同一条直线上,
∴∠AOB=180°,
∴∠AOD+∠DOE+BOE=180°,
∴∠DOE=18°,
∵∠AOC=∠BOD=∠DOE+∠BOE,
∴∠AOC=2×18o=36o.
点评 本题考查了角平分线定义,对顶角相等的性质以及平角的定义,求出∠DOE的度数是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
13.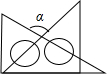 将一副三角板按如图所示摆放,图中∠α的度数是( )
将一副三角板按如图所示摆放,图中∠α的度数是( )
 将一副三角板按如图所示摆放,图中∠α的度数是( )
将一副三角板按如图所示摆放,图中∠α的度数是( )| A. | 75° | B. | 90° | C. | 120° | D. | 105° |
7.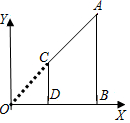 如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1),
如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1),
则△OCD与四边形ABDC的面积比为( )
 如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1),
如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1),则△OCD与四边形ABDC的面积比为( )
| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:8 |
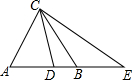 如图,△ABC中,AB=AC=8,D在AB上,E在AB的延长线上,∠ECB=∠DCB,AE=12.
如图,△ABC中,AB=AC=8,D在AB上,E在AB的延长线上,∠ECB=∠DCB,AE=12. 如果点M、N在数轴上分别表示实数m,n,在数轴上M,N两点之间的距离表示为MN=m-n(m>n)或n-m(m<n)或|m-n|.利用数形结合思想解决下列问题:已知数轴上点A与点B的距离为16个单位长度,点A在原点的左侧,到原点的距离为26个单位长度,点B在点A的右侧,点C表示的数与点B表示的数互为相反数,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
如果点M、N在数轴上分别表示实数m,n,在数轴上M,N两点之间的距离表示为MN=m-n(m>n)或n-m(m<n)或|m-n|.利用数形结合思想解决下列问题:已知数轴上点A与点B的距离为16个单位长度,点A在原点的左侧,到原点的距离为26个单位长度,点B在点A的右侧,点C表示的数与点B表示的数互为相反数,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4. 如图,点A,B,C都在格点上,请按要求回答问题或画图:
如图,点A,B,C都在格点上,请按要求回答问题或画图: