题目内容
17.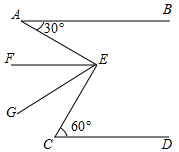 如图,AB∥CD,∠BAE=30°,∠ECD=60°,EF、EG等分∠AEC,试判断EF与AB的关系并写出你的理由.
如图,AB∥CD,∠BAE=30°,∠ECD=60°,EF、EG等分∠AEC,试判断EF与AB的关系并写出你的理由.
分析 先延长CE交AB于H,根据平行线的性质,得出∠AHE=60°,再根据三角形外角性质,得出∠AEC=∠A+∠AHE=90°,根据EF、EG等分∠AEC,得到∠AEF=$\frac{1}{3}$∠AEC=30°,最后根据∠A=∠AEF,即可判定AB∥EF.
解答 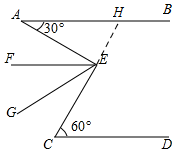 解:EF与AB互相平行.
解:EF与AB互相平行.
理由:延长CE交AB于H,
∵AB∥CD,
∴∠C=∠AHE=60°,
∵∠AEC是△AEH的外角,
∴∠AEC=∠A+∠AHE=30°+60°=90°,
又∵EF、EG等分∠AEC,
∴∠AEF=$\frac{1}{3}$∠AEC=30°,
∴∠A=∠AEF,
∴AB∥EF.
点评 本题主要考查了平行线的判定与性质的综合应用,解题时注意:两直线平行,内错角相等;内错角相等,两直线平行.解决问题的关键是作辅助线,根据三角形外角性质求得∠AEC的度数.

练习册系列答案
相关题目
7.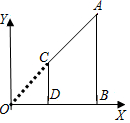 如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1),
如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1),
则△OCD与四边形ABDC的面积比为( )
 如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1),
如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1),则△OCD与四边形ABDC的面积比为( )
| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:8 |
20.下列命题是真命题的是( )
| A. | 同旁内角互补 | |
| B. | 一个角的补角大于这个角 | |
| C. | 同位角不相等,两直线不平行 | |
| D. | 如果两个角不相等,那么这两个角不是对顶角 |
1.计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与进制的数的对应关系如表:
例如,用十六进制表示5+A=F,3+F=12,E+D=1B,那么A+F=( )
| 16进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 10进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| A. | 1C | B. | 1A | C. | 19 | D. | 21 |
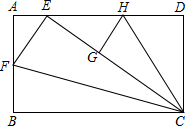 如图矩形ABCD是一张标准纸,长BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF对折使点B恰好落在边AD上的点E处,再把△DCH沿CH对折使点D落在线段CE上的点G处.
如图矩形ABCD是一张标准纸,长BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF对折使点B恰好落在边AD上的点E处,再把△DCH沿CH对折使点D落在线段CE上的点G处. 如图,点A,B,C都在格点上,请按要求回答问题或画图:
如图,点A,B,C都在格点上,请按要求回答问题或画图: