题目内容
7.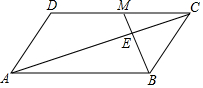 如图,在?ABCD中,∠ABC的平分线与对角线AC交于点E,与CD交于点M,已知BC=2,DM=3,?ABCD的面积为28,则△ABE的面积为( )
如图,在?ABCD中,∠ABC的平分线与对角线AC交于点E,与CD交于点M,已知BC=2,DM=3,?ABCD的面积为28,则△ABE的面积为( )| A. | $\frac{28}{3}$ | B. | $\frac{21}{2}$ | C. | 10 | D. | $\frac{14}{3}$ |
分析 由平行四边形的性质得出AD=BC=2,AB∥CD,AB=CD,△ABC的面积=14,由平行线的性质和角平分线定义证出∠CMB=∠CBM,得出MC=BC=2,求出AB=CD=MC+DM=5,由平行线证明△ABE∽△CME,得出$\frac{AE}{CE}=\frac{AB}{CM}$=$\frac{5}{2}$,求出$\frac{{S}_{△ABE}}{{S}_{△CBE}}$=$\frac{5}{2}$,即可求出△ABE的面积.
解答 解:∵四边形ABCD是平行四边形,?ABCD的面积为28,
∴AD=BC=2,AB∥CD,AB=CD,△ABC的面积=$\frac{1}{2}$×28=14,
∴∠ABM=∠CMB,
∵∠ABC的平分线为BM,
∴∠ABM=∠CBM,
∴∠CMB=∠CBM,
∴MC=BC=2,
∴AB=CD=MC+DM=5,
∵AB∥CD,
∴△ABE∽△CME,
∴$\frac{AE}{CE}=\frac{AB}{CM}$=$\frac{5}{2}$,
∴$\frac{{S}_{△ABE}}{{S}_{△CBE}}$=$\frac{5}{2}$,
∴△ABE的面积=$\frac{5}{7}$×14=10;
故选:C.
点评 本题考查了平行四边形的性质,等腰三角形的判定,相似三角形的判定与性质以及三角形的面积关系;熟练掌握平行四边形的性质,证明MC=BC和三角形相似是解决问题的关键.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
11.一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车.已知过去两次租用这两种货车的情况如表:
现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算.问:货主应付费多少元?
| 第一次 | 第二次 | |
| 甲种货车辆数(单位:辆) | 2 | 5 |
| 乙种货车辆数(单位:辆) | 3 | 6 |
| 累计货运吨数(单位:吨) | 15.5 | 35 |
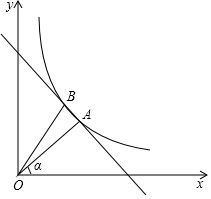 如图,在坐标系中,线段OA在第一象限,OA=5,OA与x轴的夹角α的正切tanα=$\frac{3}{4}$,反比例函数y=$\frac{k}{x}$(k≠0,x>0)图象经过点A,OA绕点O旋转后落在反比例函数y=$\frac{k}{x}$(x>0)的图象上另一点B,点B与x轴距离是4.
如图,在坐标系中,线段OA在第一象限,OA=5,OA与x轴的夹角α的正切tanα=$\frac{3}{4}$,反比例函数y=$\frac{k}{x}$(k≠0,x>0)图象经过点A,OA绕点O旋转后落在反比例函数y=$\frac{k}{x}$(x>0)的图象上另一点B,点B与x轴距离是4.
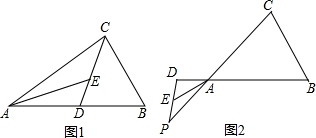
 如图,点A,B,C都在格点上,请按要求回答问题或画图:
如图,点A,B,C都在格点上,请按要求回答问题或画图: 如图,已知∠ADE=∠B,∠CDE=∠BFG,求证:FG∥CD.
如图,已知∠ADE=∠B,∠CDE=∠BFG,求证:FG∥CD.