题目内容
11.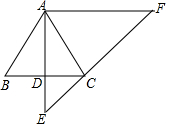 已知:如图,在△ABC中,AB=AC,过点A作AD⊥BC,垂足为点D,延长AD至点E,使DE=$\frac{1}{2}$AD,过点A作AF∥BC,交EC的延长线于点F.
已知:如图,在△ABC中,AB=AC,过点A作AD⊥BC,垂足为点D,延长AD至点E,使DE=$\frac{1}{2}$AD,过点A作AF∥BC,交EC的延长线于点F.(1)设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,用$\overrightarrow{a}$、$\overrightarrow{b}$的线性组合表示$\overrightarrow{AE}$;
(2)求$\frac{{S}_{△DEC}}{{S}_{△AFC}}$的值.
分析 (1)由平面向量的三角形法则得到$\overrightarrow{AD}$,然后结合已知条件DE=$\frac{1}{2}$AD来求$\overrightarrow{AE}$;
(2)根据平行线截线段成比例和三角形的面积公式进行解答.
解答  解:(1)∵如图,在△ABC中,AB=AC,AD⊥BC,
解:(1)∵如图,在△ABC中,AB=AC,AD⊥BC,
∴BD=$\frac{1}{2}$BC,
∵$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,
∴$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$=$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$.
又∵DE=$\frac{1}{2}$AD,
∴$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$,
∴$\overrightarrow{AE}$=$\overrightarrow{AD}$+$\overrightarrow{DE}$=$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$=$\frac{3}{2}$$\overrightarrow{a}$+$\frac{3}{4}$$\overrightarrow{b}$;
(2)∵DE=$\frac{1}{2}$AD,AF∥BC,
∴$\frac{DE}{AD}$=$\frac{1}{2}$,$\frac{DC}{AF}$=$\frac{ED}{AE}$=$\frac{1}{3}$,
∴$\frac{{S}_{△DEC}}{{S}_{△AFC}}$=$\frac{\frac{1}{2}DC•DE}{\frac{1}{2}AF•AD}$=$\frac{DC}{AF}$•$\frac{DE}{AD}$=$\frac{1}{3}$×$\frac{1}{2}$=$\frac{1}{6}$,
即$\frac{{S}_{△DEC}}{{S}_{△AFC}}$=$\frac{1}{6}$.
点评 本题考查了平面向量和等腰三角形的性质.解答关于平面向量的问题时,一般采用“数形结合”的数学思想.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | tanB=$\frac{2}{3}$ | B. | cotB=$\frac{2}{3}$ | C. | sinB=$\frac{2}{3}$ | D. | cosB=$\frac{2}{3}$ |
| A. | |${\overrightarrow b}$|=2|$\overrightarrow a}$| | B. | 2$\overrightarrow a+\overrightarrow b=0$ | C. | $\overrightarrow b∥\overrightarrow a$ | D. | $\overrightarrow b≠\overrightarrow a$ |
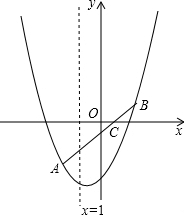 如图,已知:A(-2,-3),C(0,-1),B点与A点关于C点中心对称,抛物线y=ax2+bx+c过A、B两点且对称轴为x=-1.
如图,已知:A(-2,-3),C(0,-1),B点与A点关于C点中心对称,抛物线y=ax2+bx+c过A、B两点且对称轴为x=-1.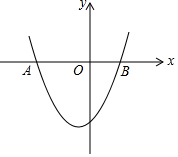 如图,已知抛物线y=x2+x-6与x轴两个交点分别是A、B(点A在点B的左侧).
如图,已知抛物线y=x2+x-6与x轴两个交点分别是A、B(点A在点B的左侧).