题目内容
19.如果在Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式正确的是( )| A. | tanB=$\frac{2}{3}$ | B. | cotB=$\frac{2}{3}$ | C. | sinB=$\frac{2}{3}$ | D. | cosB=$\frac{2}{3}$ |
分析 根据勾股定理求出AB,根据锐角三角函数的定义计算即可判断.
解答 解:∵∠C=90°,AC=2,BC=3,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{13}$,
∴tanB=$\frac{AC}{BC}$=$\frac{2}{3}$,
cotB=$\frac{BC}{AC}$=$\frac{3}{2}$,
sinB=$\frac{AC}{AB}$=$\frac{2\sqrt{13}}{13}$,
cosB=$\frac{BC}{AC}$=$\frac{3\sqrt{13}}{13}$,
故选:A/.
点评 本题考查的是锐角三角函数的定义,掌握一个锐角的四个三角函数的定义是解题的关键.

练习册系列答案
相关题目
10.已知关于x的分式方程$\frac{1-m}{x-1}$-1=$\frac{2}{1-x}$的解是正数,则m的取值范围是( )
| A. | m<4且m≠3 | B. | m<4 | C. | m≤4且m≠3 | D. | m>5且m≠6 |
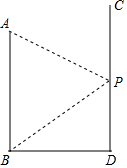 如图,AB、CD分别表示两幢相距36米的大楼,高兴同学站在CD大楼的P处窗口观察AB大楼的底部B点的俯角为45°,观察AB大楼的顶部A点的仰角为30°,求大楼AB的高.
如图,AB、CD分别表示两幢相距36米的大楼,高兴同学站在CD大楼的P处窗口观察AB大楼的底部B点的俯角为45°,观察AB大楼的顶部A点的仰角为30°,求大楼AB的高.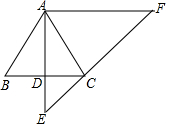 已知:如图,在△ABC中,AB=AC,过点A作AD⊥BC,垂足为点D,延长AD至点E,使DE=$\frac{1}{2}$AD,过点A作AF∥BC,交EC的延长线于点F.
已知:如图,在△ABC中,AB=AC,过点A作AD⊥BC,垂足为点D,延长AD至点E,使DE=$\frac{1}{2}$AD,过点A作AF∥BC,交EC的延长线于点F.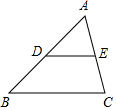 如图,在△ABC中,点D,E分别是边AB,AC的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.
如图,在△ABC中,点D,E分别是边AB,AC的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$. 如图,∠A的同位角是∠BEC.
如图,∠A的同位角是∠BEC.