题目内容
5.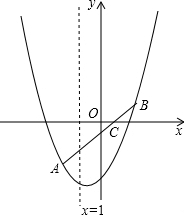 如图,已知:A(-2,-3),C(0,-1),B点与A点关于C点中心对称,抛物线y=ax2+bx+c过A、B两点且对称轴为x=-1.
如图,已知:A(-2,-3),C(0,-1),B点与A点关于C点中心对称,抛物线y=ax2+bx+c过A、B两点且对称轴为x=-1.(1)求抛物线的解析式;
(2)在直线AB下方的抛物线上求一点P,使△ABP的面积最大,求出P点的坐标和△ABP面积的最大值.
分析 (1)由题意求出B坐标,再由对称轴方程,求出a,b,c的值,即可确定出解析式;
(2)过P作PQ⊥x轴,交AB于点Q,设P坐标为(m,$\frac{1}{2}$m2+m-4),表示出Q(m,m-1),进而表示出PQ,三角形ABP面积=三角形APQ面积+三角形BPQ面积,列出二次函数解析式,利用二次函数性质求出面积最大值,以及此时P的坐标即可.
解答 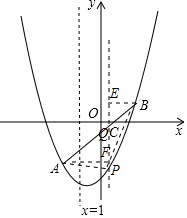 解:(1)∵A、B关于C中心对称,A(-2,-3),C(0,-1),
解:(1)∵A、B关于C中心对称,A(-2,-3),C(0,-1),
∴B(2,1),
由抛物线对称轴为x=-1,得到$\left\{\begin{array}{l}{-\frac{b}{2a}=-1}\\{4a-2b+c=-3}\\{4a+2b+c=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=1}\\{c=-3}\end{array}\right.$,
则抛物线解析式为y=$\frac{1}{2}$x2+x-3;
(2)过P作PQ⊥x轴,交AB于点Q,AF⊥PQ,BE⊥PQ,
设P坐标为(m,$\frac{1}{2}$m2+m-4),则Q(m,m-1),
∴PQ=m-1-$\frac{1}{2}$m2-m+4=-$\frac{1}{2}$m2+3,
∴S△ABP=S△APQ+S△BPQ=$\frac{1}{2}$PQ•AF+$\frac{1}{2}$PQ•BE=$\frac{1}{2}$PQ•(AF+BE)=$\frac{1}{2}$•(-$\frac{1}{2}$m2+3)•(2+2)=-m2+6,
∵a=-1<0,
∴S△ABP有最大值,当m=3时,S△ABP最大值为6,此时P坐标为(3,$\frac{7}{2}$).
点评 此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | m<4且m≠3 | B. | m<4 | C. | m≤4且m≠3 | D. | m>5且m≠6 |
| A. | y1<y2<y3 | B. | y2<y3<y1 | C. | y3<y2<y1 | D. | y1<y3<y2 |
| A. | -2 | B. | 3 | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}$ |
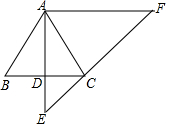 已知:如图,在△ABC中,AB=AC,过点A作AD⊥BC,垂足为点D,延长AD至点E,使DE=$\frac{1}{2}$AD,过点A作AF∥BC,交EC的延长线于点F.
已知:如图,在△ABC中,AB=AC,过点A作AD⊥BC,垂足为点D,延长AD至点E,使DE=$\frac{1}{2}$AD,过点A作AF∥BC,交EC的延长线于点F.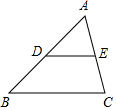 如图,在△ABC中,点D,E分别是边AB,AC的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.
如图,在△ABC中,点D,E分别是边AB,AC的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$. 如图,∠A的同位角是∠BEC.
如图,∠A的同位角是∠BEC.