题目内容
11.若用半径为2,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是$\frac{2}{3}$.分析 根据图形可知,圆锥的侧面展开图为扇形,且其弧长等于圆锥底面圆的周长.
解答  解:设这个圆锥的底面半径是R,则有:
解:设这个圆锥的底面半径是R,则有:
2πR=120π×$\frac{2}{180}$,
解得:R=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 此题考查了圆锥侧面展开扇形与底面圆之间的关系,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
6.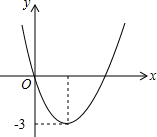 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有两个相等的实数根,则m的值为( )
二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有两个相等的实数根,则m的值为( )
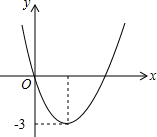 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有两个相等的实数根,则m的值为( )
二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx=m有两个相等的实数根,则m的值为( )| A. | -3 | B. | 3 | C. | -6 | D. | 9 |
16.将抛物线y1=-x2平移后得到y2=-x2+2x-2,则把抛物线y1平移到y2的方法是( )
| A. | 先向左平移1个单位,再向下平移1个单位 | |
| B. | 先向左平移1个单位,再向上平移1个单位 | |
| C. | 先向右平移1个单位,再向下平移1个单位 | |
| D. | 先向有平移1个单位,再向上平移1个单位 |
20. 如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1、B2、B3、…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=2,则点B2011的坐标是( )
如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1、B2、B3、…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=2,则点B2011的坐标是( )
 如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1、B2、B3、…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=2,则点B2011的坐标是( )
如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1、B2、B3、…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=2,则点B2011的坐标是( )| A. | (22010,22010) | B. | (22011,22011) | C. | (22010,22011) | D. | (22011,22012) |
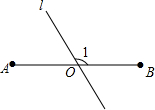 如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=3或3$\sqrt{3}$或3$\sqrt{7}$.
如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=3或3$\sqrt{3}$或3$\sqrt{7}$. 如图,A点为反比例函数$y=\frac{k}{x}$图象上一点,过A点作AB⊥y轴,B为垂足,点P为x轴上任意一点,且△ABP的面积为2,则k=-4.
如图,A点为反比例函数$y=\frac{k}{x}$图象上一点,过A点作AB⊥y轴,B为垂足,点P为x轴上任意一点,且△ABP的面积为2,则k=-4. 如图,已知反比例函数y=$\frac{6}{x}$的图象与正比例函数y=$\frac{2}{3}$x的图象交于A、B两点,B点坐标为(-3,-2),则A点的坐标为(3,2)
如图,已知反比例函数y=$\frac{6}{x}$的图象与正比例函数y=$\frac{2}{3}$x的图象交于A、B两点,B点坐标为(-3,-2),则A点的坐标为(3,2)