题目内容
6．
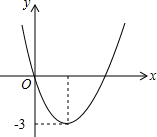二次函数y=ax2+bx的图象如图，若一元二次方程ax2+bx=m有两个相等的实数根，则m的值为（ ）| A． | -3 | B． | 3 | C． | -6 | D． | 9 |
分析 直接利用一元二次方程隔得判别式得出b2+4am=0，进而利用二次函数顶点坐标得出m的值．
解答 解：∵一元二次方程ax2+bx=m有两个相等的实数根，
∴b2+4am=0，
∵y=ax2+bx的顶点坐标纵坐标为：$\frac{-{b}^{2}}{4a}$=-3，
则b2=12a，
故12a+4am=0，
则m=-3．
故选：A．
点评 此题主要考查了抛物线与x轴的交点，正确得出a，b的关系是解题关键．
练习册系列答案
相关题目
如图，反比例函数y=$\frac{4}{x}$的图象与一次函数y=kx-3的图象在第一象限内相交于点A，且点A的横坐标为4．
如图，在平行四边形ABCD中，点E、F分别在AB、AD上，且AE=$\frac{1}{3}$AB，AF=$\frac{1}{4}$AD，连结EF交对角线AC于G，则$\frac{AG}{AC}$=$\frac{1}{7}$．
1．线段CD是由线段AB平移得到的，点A（-2，5）的对应点为C（3，7），则点B（-4，-7）的对应点D的坐标为（ ）
| A． | （2，9） | B． | （5，2） | C． | （1，-5） | D． | （-9，-5） |
如图，在?ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF，CF．在不添加辅助线的情况下，请写出与∠AEF相等的所有角∠DCF，∠BCF，∠DFC．