题目内容
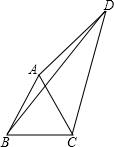 在四边形ABCD中,△ABC是等边三角形,∠ADC=30°,AD=3,BD=2
在四边形ABCD中,△ABC是等边三角形,∠ADC=30°,AD=3,BD=2| 6 |
考点:全等三角形的判定与性质,等边三角形的性质,勾股定理
专题:
分析:以DC为边作等边三角形DCE,易证∠ACE=∠BCD,即可证明△BCD≌△ACE,可得BD=AE,易证∠ADE=90°,根据勾股定理即可求得DE的长,即可解题.
解答:解:以DC为边作等边三角形DCE,
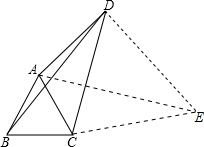
∵△ABC,△DCE是等边三角形,∴AC=BC,CD=CE,
∵∠ACB=∠DCE=60°,∴∠ACB+∠ACD=∠DCE+∠ACD,
∴∠ACE=∠BCD,
∵在△BCD和△ACE中,
,
∴△BCD≌△ACE,(SAS)
∴BD=AE,
∵∠ADC=30°,∠CDE=60°,
∴∠ADE=90°,
∴DE2=AE2-AD2=BD2-AD2=15,
∴CD=DE=
.
故答案为
.

∵△ABC,△DCE是等边三角形,∴AC=BC,CD=CE,
∵∠ACB=∠DCE=60°,∴∠ACB+∠ACD=∠DCE+∠ACD,
∴∠ACE=∠BCD,
∵在△BCD和△ACE中,
|
∴△BCD≌△ACE,(SAS)
∴BD=AE,
∵∠ADC=30°,∠CDE=60°,
∴∠ADE=90°,
∴DE2=AE2-AD2=BD2-AD2=15,
∴CD=DE=
| 15 |
故答案为
| 15 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了直角三角形中勾股定理的运用,本题中求证△BCD≌△ACE是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 已知DE∥BC,FG⊥AB,∠1=∠2,求证:CD⊥AB.
已知DE∥BC,FG⊥AB,∠1=∠2,求证:CD⊥AB. 如图,△ABC绕点A顺时针旋转60°得到△AEF,若∠B=100°,∠F=50°,则∠CAE的度数为
如图,△ABC绕点A顺时针旋转60°得到△AEF,若∠B=100°,∠F=50°,则∠CAE的度数为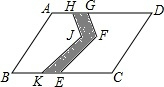 如图,在平行四边形ABCD这块土地上,有一条小路(阴影部分),现要把它改为经过点E的直路,并保持小路两侧土地的面积不变,请在图中画出你设计的小路,并说明理由.
如图,在平行四边形ABCD这块土地上,有一条小路(阴影部分),现要把它改为经过点E的直路,并保持小路两侧土地的面积不变,请在图中画出你设计的小路,并说明理由. 已知,如图,AB为⊙O的直径,E为⊙O外一点,EB,EC分别切⊙O于点B,C,求证:AC∥OE.
已知,如图,AB为⊙O的直径,E为⊙O外一点,EB,EC分别切⊙O于点B,C,求证:AC∥OE.