题目内容
 已知AB是⊙O的直径,AD与⊙O相交,点C是⊙O上一点,经过点C的直线交AD于点E,如图.若CE是⊙O的切线,AC平分∠BAD,AB=8,AC=6.求AD的长.
已知AB是⊙O的直径,AD与⊙O相交,点C是⊙O上一点,经过点C的直线交AD于点E,如图.若CE是⊙O的切线,AC平分∠BAD,AB=8,AC=6.求AD的长.考点:切线的性质
专题:
分析:连接OC,BC,首先证明AD∥OC,即可证得∠D=90°,然后证明△DAC∽△CAB,根据相似三角形的对应边的比相等即可求解.
解答: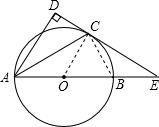 解:连接OC,BC.
解:连接OC,BC.
∵CE是圆的切线,
∴OC⊥CD,
∵AC平分∠BAD,即∠DAC=∠CAE,
又∵OA=OC,
∴∠CAE=∠ACO,
∴∠DAC=∠ACO,
∴AD∥OC,
∴AD⊥DC,即∠D=∠OCE,
∵AB是圆的直径,
∴∠ACB=90°,
∴∠D=∠ACB,
又∵∠DAC=∠CAE,
∴△DAC∽△CAB,
∴
=
,即
=
,
解得:AC=
.
 解:连接OC,BC.
解:连接OC,BC.∵CE是圆的切线,
∴OC⊥CD,
∵AC平分∠BAD,即∠DAC=∠CAE,
又∵OA=OC,
∴∠CAE=∠ACO,
∴∠DAC=∠ACO,
∴AD∥OC,
∴AD⊥DC,即∠D=∠OCE,
∵AB是圆的直径,
∴∠ACB=90°,
∴∠D=∠ACB,
又∵∠DAC=∠CAE,
∴△DAC∽△CAB,
∴
| AD |
| AC |
| AC |
| AB |
| AD |
| 6 |
| 6 |
| 8 |
解得:AC=
| 9 |
| 2 |
点评:本题考查了切线的性质、圆周角定理以及相似三角形的判定与性质,证明△DAC∽△CAB是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,一个长为5cm、宽为lcm的长方形,你能否将它剪成五块拼成一个正方形?若能,请画出剪裁和拼凑方案,并求正方形边长.
如图,一个长为5cm、宽为lcm的长方形,你能否将它剪成五块拼成一个正方形?若能,请画出剪裁和拼凑方案,并求正方形边长.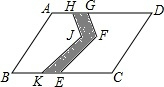 如图,在平行四边形ABCD这块土地上,有一条小路(阴影部分),现要把它改为经过点E的直路,并保持小路两侧土地的面积不变,请在图中画出你设计的小路,并说明理由.
如图,在平行四边形ABCD这块土地上,有一条小路(阴影部分),现要把它改为经过点E的直路,并保持小路两侧土地的面积不变,请在图中画出你设计的小路,并说明理由.